application-of-derivatives-3
Rolle's Theorem:
Statement: Let f be real valued function defined on closed interval [a, b] such that,
(i) f(x) is continuous in closed interval [a, b].
(ii) f(x) is differentiable in open interval (a, b).
(iii) f(a) = f(b)
Then there is at least one value of C of x in (a, b) for which f'(c) = 0
Proof: Case I: f(x) is constant function in interval [a, b] then f'(x) = 0 for all x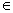 [a, b]
[a, b]
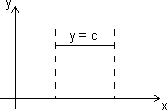
Hence, follows Rolle's theorem, we can say that f'(c) = 0 where a < c < b.
Case II: f(x) is not constant in interval [a, b] & sionce f(a) = f(b)
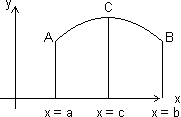
Let f(x) increases for x > a.
Since f(a) = f(b), so, function must increase to some value x = c & decreasing upto x = b.
 At x = c function has maximum value.
At x = c function has maximum value.
Let h be small quantity, then,
f(c + h) - f(c) < 0 & f(c - h) - f(c) < 0
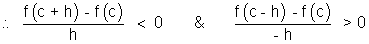
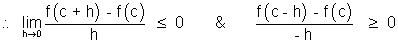
But if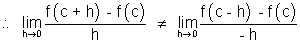
Then Rolle's theorem cannot applicable b/c. f(x) is not differentiable at x = c
 Only possible way for Rolle's theorem, when
Only possible way for Rolle's theorem, when
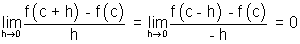
 f'(c) = 0 where a < c < b
f'(c) = 0 where a < c < b
Note: (i) Polynomial function is everywhere cont. & differentiable.
(ii) Exponential function, sine & cosine function are everywhere cont. & differentiable.
(iii) Logarithmic function is cont. & differentiable in its domain.
(iv) tanx is not cont. & differentiable at x = ±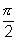 , ±
, ±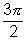 , ...............
, ...............
(v) |x| is not differentiable at x = 0.
Illustration: Verify Rolle's theorem for function f(x) = x3 - 3x2 + 2x in interval [0, 2].
Ans: (a) f(x) is polynomial so, it is cont. & differentiable everywhere.
(b) f'(x) = 3x2 - 6x + 2 clearly exista for all x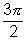 (0,2)
(0,2)
(c) f(0) = 0, f(2) = 23 - 3(2)2 + 2(2) = 0
 f(0) = f(2)
f(0) = f(2)
So, All conditions of Rolle's theorem are satisfied.
So, there exist some c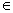 (0,2) such that f'(c) = 0
(0,2) such that f'(c) = 0
 f'(c) = 3c2 - 6c + 2 = 0
f'(c) = 3c2 - 6c + 2 = 0  c = 1 ±
c = 1 ± 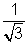
Lagrange's Mean Value Theorem:
Statement:
(i) f(x) is cont. in closed interval [a, b].
(ii) is differentiable in open interval (a, b)
Then there is at least one value c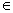 (a, b) such that
(a, b) such that
f'(c) =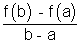
Geometrical interpretation:
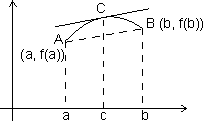
Let A, B be points on curve y = f(x) corresponding to x = a & x = b, so that
A = [a, f(a)] & B = [b, f(b)]
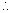 Slope of chord AB =
Slope of chord AB = 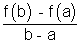
But slope of chord AB = f'(c), the slope of tangent to curve at x = c.
Accordin to LMVT, if a curve has tangent at each of its points then there is a point 'c' on this curve in between A & B, the tangent at which is paralled to chord AB.
Illustration: Find c of LMVT for which f(x) =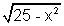 in [1, 5].
in [1, 5].
Ans: (1) f(x) has definite & unique value of each x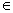 [1, 5]
[1, 5]
So, every point in interval [1, 5] the value of f(x) is equal to limit of f(x).
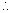 f(x) is cont. in [1, 5]
f(x) is cont. in [1, 5]
(2) f'(x) = -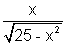 exists for all x
exists for all x 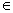 [1, 5]
[1, 5]
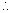 f(x) is differentiable in (1, b)
f(x) is differentiable in (1, b)
So, there must br some c such that
f'(c) =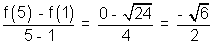
But f'(c) =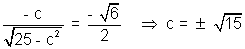
Application of derivative in determining the nature of roots of cubic polynomial:
Let f(x) = x3 + ax2 + bx + c be given cubic polynomial.
 f(x) = 0
f(x) = 0
f'(x) = 3x2 + 2ax + b ....................................................... (i)
Let D = 4a2 - 12b = 4(a2 - 3b) be discriminate of eq. f'(x) = 0
Case I: If D < 0 f'(x) > 0
f'(x) > 0 v x 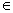 R
R
 f(x) = -
f(x) = - 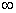 and
and 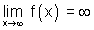
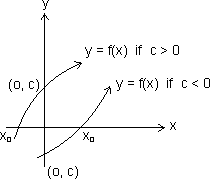
from fig. graph of y = f(x) cut x-axis only once. So, we have only real root (say x0)
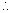 x0 > 0 if c < 0 & x0 < 0 if c > 0
x0 > 0 if c < 0 & x0 < 0 if c > 0
Case II: If D > 0, f'(x) = 0
have two real roots.
 f'(x) = 3(x - x1)(x - x2)
f'(x) = 3(x - x1)(x - x2)
f'(x) < 0, x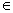 (x1, x2)
(x1, x2)
f'(x) > 0, x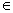 (-
(- 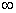 , x1) U (x2,
, x1) U (x2, 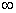 )
)
 f(x) would increase in (-
f(x) would increase in (-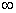 , x1) & (x2,
, x1) & (x2, 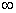 ) and would decrese in (x1, x2)
) and would decrese in (x1, x2)
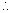 x = x1 would be point of local maxima & x = x2 would be point of local minima.
x = x1 would be point of local maxima & x = x2 would be point of local minima.
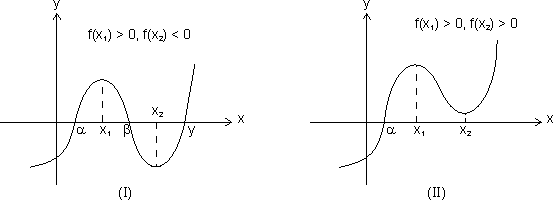
3 distict roots x =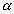 ,
,  ,
,  One real root x =
One real root x = 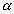 & two imaginary root
& two imaginary root
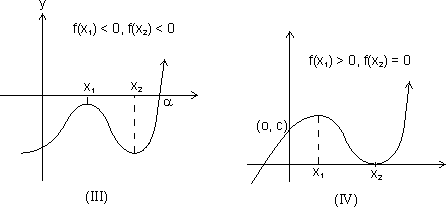
One real root x = 9 & Three roots x =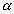 , n2, x2
, n2, x2
two imaginary roots. (x2 is repeated root)
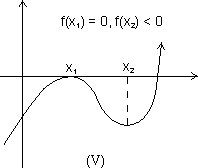
Results:
(a) From I graph, f(x1) > 0, f(x2) < 0
 f(x1) f(x2) < 0, f(x) = 0 would have 3 real & distinct roots.
f(x1) f(x2) < 0, f(x) = 0 would have 3 real & distinct roots.
(b) Fromn II & III graph f(x1) f(x2) > 0, f(x) = 0 have one real & two imaginary roots.
(c) f(x1 f(x2) = 0, f(x) = 0 have 3 real roots but of root would be repeated.
Case III: D = 0, f'(x) = 3(x - x1)0 where x1 is root of f'(x).
 f(x) = (x - x1)3 + K
f(x) = (x - x1)3 + K
Then, f(x) = 0, has three real roots if K = 0
f(x) = 0 has one real root if K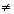 0
0
Illustration: Find values of a so that x3 - 3x + a = 0 has three real & distinct roots.
Ans: Let f(x) = 3x3 - 3x + a
 f'(x) = 3x2 - 3 = 3(x - 1)(x + 1)
f'(x) = 3x2 - 3 = 3(x - 1)(x + 1)
x1 = 1, x2 = - 1
f(x1) = f(1) = a - 2
f(x2) = f(- 1) = a + 2
Since roots would be real & distinct if
f(1) f(- 1) < 0 (a - 2)(a + 2) < 0
(a - 2)(a + 2) < 0
 - 2 < a < 2
- 2 < a < 2
Statement: Let f be real valued function defined on closed interval [a, b] such that,
(i) f(x) is continuous in closed interval [a, b].
(ii) f(x) is differentiable in open interval (a, b).
(iii) f(a) = f(b)
Then there is at least one value of C of x in (a, b) for which f'(c) = 0
Proof: Case I: f(x) is constant function in interval [a, b] then f'(x) = 0 for all x
 [a, b]
[a, b] 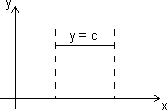
Hence, follows Rolle's theorem, we can say that f'(c) = 0 where a < c < b.
Case II: f(x) is not constant in interval [a, b] & sionce f(a) = f(b)

Let f(x) increases for x > a.
Since f(a) = f(b), so, function must increase to some value x = c & decreasing upto x = b.
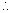 At x = c function has maximum value.
At x = c function has maximum value. Let h be small quantity, then,
f(c + h) - f(c) < 0 & f(c - h) - f(c) < 0
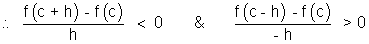
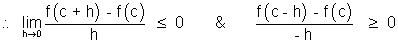
But if
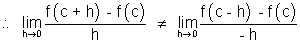
Then Rolle's theorem cannot applicable b/c. f(x) is not differentiable at x = c
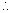 Only possible way for Rolle's theorem, when
Only possible way for Rolle's theorem, when 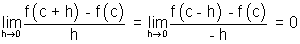
 f'(c) = 0 where a < c < b
f'(c) = 0 where a < c < b Note: (i) Polynomial function is everywhere cont. & differentiable.
(ii) Exponential function, sine & cosine function are everywhere cont. & differentiable.
(iii) Logarithmic function is cont. & differentiable in its domain.
(iv) tanx is not cont. & differentiable at x = ±
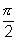 , ±
, ±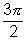 , ...............
, ............... (v) |x| is not differentiable at x = 0.
Illustration: Verify Rolle's theorem for function f(x) = x3 - 3x2 + 2x in interval [0, 2].
Ans: (a) f(x) is polynomial so, it is cont. & differentiable everywhere.
(b) f'(x) = 3x2 - 6x + 2 clearly exista for all x
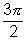 (0,2)
(0,2)(c) f(0) = 0, f(2) = 23 - 3(2)2 + 2(2) = 0
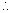 f(0) = f(2)
f(0) = f(2) So, All conditions of Rolle's theorem are satisfied.
So, there exist some c
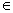 (0,2) such that f'(c) = 0
(0,2) such that f'(c) = 0  f'(c) = 3c2 - 6c + 2 = 0
f'(c) = 3c2 - 6c + 2 = 0  c = 1 ±
c = 1 ± 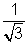
Lagrange's Mean Value Theorem:
Statement:
(i) f(x) is cont. in closed interval [a, b].
(ii) is differentiable in open interval (a, b)
Then there is at least one value c
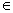 (a, b) such that
(a, b) such that f'(c) =
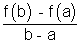
Geometrical interpretation:

Let A, B be points on curve y = f(x) corresponding to x = a & x = b, so that
A = [a, f(a)] & B = [b, f(b)]
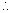 Slope of chord AB =
Slope of chord AB = 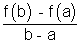
But slope of chord AB = f'(c), the slope of tangent to curve at x = c.
Accordin to LMVT, if a curve has tangent at each of its points then there is a point 'c' on this curve in between A & B, the tangent at which is paralled to chord AB.
Illustration: Find c of LMVT for which f(x) =
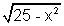 in [1, 5].
in [1, 5]. Ans: (1) f(x) has definite & unique value of each x
 [1, 5]
[1, 5] So, every point in interval [1, 5] the value of f(x) is equal to limit of f(x).
 f(x) is cont. in [1, 5]
f(x) is cont. in [1, 5] (2) f'(x) = -
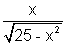 exists for all x
exists for all x 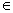 [1, 5]
[1, 5]  f(x) is differentiable in (1, b)
f(x) is differentiable in (1, b) So, there must br some c such that
f'(c) =
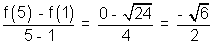
But f'(c) =
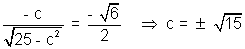
Application of derivative in determining the nature of roots of cubic polynomial:
Let f(x) = x3 + ax2 + bx + c be given cubic polynomial.
 f(x) = 0
f(x) = 0 f'(x) = 3x2 + 2ax + b ....................................................... (i)
Let D = 4a2 - 12b = 4(a2 - 3b) be discriminate of eq. f'(x) = 0
Case I: If D < 0
 f'(x) > 0
f'(x) > 0 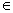 R
R  f(x) = -
f(x) = - 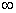 and
and 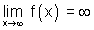
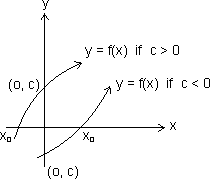
from fig. graph of y = f(x) cut x-axis only once. So, we have only real root (say x0)
 x0 > 0 if c < 0 & x0 < 0 if c > 0
x0 > 0 if c < 0 & x0 < 0 if c > 0 Case II: If D > 0, f'(x) = 0
have two real roots.
 f'(x) = 3(x - x1)(x - x2)
f'(x) = 3(x - x1)(x - x2) f'(x) < 0, x
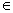 (x1, x2)
(x1, x2) f'(x) > 0, x
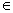 (-
(-  , x1) U (x2,
, x1) U (x2, 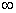 )
)  f(x) would increase in (-
f(x) would increase in (-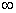 , x1) & (x2,
, x1) & (x2, 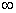 ) and would decrese in (x1, x2)
) and would decrese in (x1, x2) 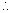 x = x1 would be point of local maxima & x = x2 would be point of local minima.
x = x1 would be point of local maxima & x = x2 would be point of local minima. 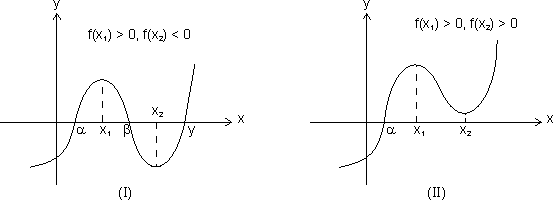
3 distict roots x =
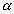 ,
,  ,
,  One real root x =
One real root x = 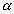 & two imaginary root
& two imaginary root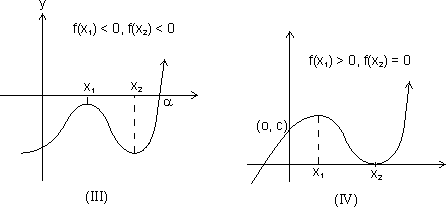
One real root x = 9 & Three roots x =
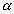 , n2, x2
, n2, x2two imaginary roots. (x2 is repeated root)
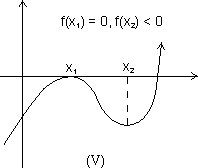
Threen real roots x = n1, x2, 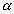
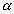
(x1 is repeated roots)
Results:
(a) From I graph, f(x1) > 0, f(x2) < 0
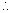 f(x1) f(x2) < 0, f(x) = 0 would have 3 real & distinct roots.
f(x1) f(x2) < 0, f(x) = 0 would have 3 real & distinct roots. (b) Fromn II & III graph f(x1) f(x2) > 0, f(x) = 0 have one real & two imaginary roots.
(c) f(x1 f(x2) = 0, f(x) = 0 have 3 real roots but of root would be repeated.
Case III: D = 0, f'(x) = 3(x - x1)0 where x1 is root of f'(x).
 f(x) = (x - x1)3 + K
f(x) = (x - x1)3 + K Then, f(x) = 0, has three real roots if K = 0
f(x) = 0 has one real root if K
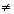 0
0 Illustration: Find values of a so that x3 - 3x + a = 0 has three real & distinct roots.
Ans: Let f(x) = 3x3 - 3x + a
 f'(x) = 3x2 - 3 = 3(x - 1)(x + 1)
f'(x) = 3x2 - 3 = 3(x - 1)(x + 1) x1 = 1, x2 = - 1
f(x1) = f(1) = a - 2
f(x2) = f(- 1) = a + 2
Since roots would be real & distinct if
f(1) f(- 1) < 0
 (a - 2)(a + 2) < 0
(a - 2)(a + 2) < 0  - 2 < a < 2
- 2 < a < 2