Q.4. If at each point of curve y = x
3 - ax
2 + x + 1 tangent is inclined at acute angle with +ve direction of x-axis. Find interval in which a lies.
Ans: y = x
3 - ax
2 + x + 1
Sine tangent is inclined at an acute angle with the direction of x-axis.
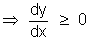
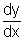
= 3x
2 - 2ax + 1
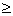
0 for all x
R
But if ax
2 + bx + c
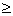
0 for x
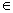
R
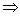
a > 0 & D
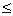
0
D = (2a)
2 - 4(3)(11)
= 4(a
2 - 3)
D
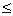
0
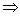
(a
2 - 3)
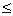
0
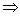
(a -
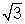
)(a +
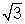
)
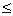
0
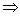
-
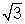
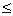
a
 Dumb Question
Dumb Question: How
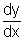
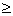
0 if angle is acute.
Ans: Since
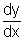
= tan
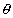
& if
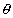
is lessthan
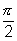
. So, tan
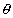
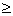
0. So,
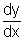
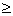
0
Q.5. If f(x) = log
ex & g(x) = x
2 & c
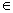
(4, 5), then find value of c log
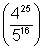
Ans: log(4
25) - log5
16
25 log4 - 16 log5
Since domain is [4, 5]
So, let
Ø(x) = x
2 (log4) - 16 logx i9s cont. [45, 5] & differentiable on (4, 5)
By LMUT,
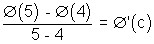
, c
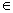
(4, 5)
Ø(5) - Ø(4) = log
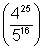
But, Ø'(c) =
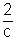
(c
2 log4 - 8) ........................................ (i)
also Ø'(c) =
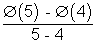
........................................... (ii)
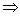
By (i) & (ii)
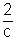
(c
2 log
e4 - 8) = log
e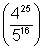
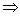
c log
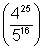
= 2(c
2 log4 - 8)
Hard Type:
Q.1. Let S be square of unit area. Consider aany quadrilateral which has one vertex on each side of s. If a, b, c, & d denote lengths of side of quadrilateral, prove that
2
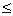
a
2 + b
2 + c
2 + d
2 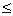
4
Ans:
Let S be square of unit area & ABCD be quadrilateral of sides a, b, c & d
a
2 = (1 - x)
2 + z
2
b
2 = w
2 + (1 - z)
2
c
2 = (1 - w)
2 + (1 - y)
2
d
2 = x
2 + y
2
a
2 + b
2 + c
2 + d
2 = {x
2 + (1 - x)
2} + {y
2 + (1 - y)
2} + {z
2 + (1 - z)
2}
+ {w
2 + (1 - w)
2}
where 0
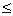
x, y, z, w
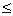
1
Let f(x) = x
2 + (1 - x)
2, 0
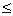
x
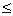
1
Then f'(x) = 2x - 2(1 - x)
f'(x) = 0 for min/max.
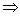
4x - 2 = 0
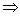
x =
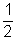
Again f''(x) = 4 > 0 when x =
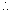
f(x) is min. at x =
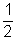
& m,ax. at x = 1
a
2 + b
2 + c
2 + d
2 = 4{x
2 + (1 - x)
2}
Max. value of x
2 + (1 - x)
2 = 1
2 + (1 - 1)
2 = 1
Min. value of x
2 + (1 - x)
2 =
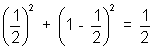
2  a2 + b2 + c2 + d2 a2 + b2 + c2 + d2  4 4 |
Q.2. Let a + b = 4 & a < 2 & let g(x) be differentiable function. If
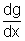
> 0
v x prove that
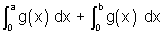
increases as (b - a) increases.
Ans: Let (b - a) = t & since a + b = 4
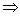
a =
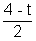
& b =
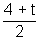
& t > 0
[
Dumb Question: Why t = b - a > 0 ?
Ans: Since a < 2 &n & a + b = 4. So, b > 2
b - a > 0 or t > 0]
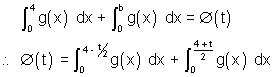
Ø(t) =
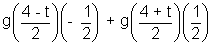
[By Leibniz rule]
[
Dumb Question: What is Leibniz rule ?
Ans: Ø(t) =
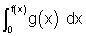
]
Ø'(t) = g(f(x)) f'(x)
Since g(x) is increasing
x
2 > x
1 
g(x
2) > g(x
1)
Now,
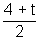
>
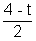
& g(x) is increasing
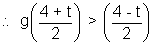
Ø'(t) =
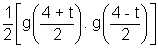
> 0
Ø'(t) > 0
Ø'(t) is increases as t increases.
Q.3. Tangent represented by graph of function y = ... at the point with absciss a x = 1 from an angle
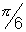
& at point x = 2 an angle of
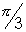
& at the point x an angle of
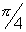
. Find value of
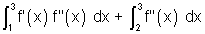
.
Ans: Given
at x = 1,
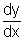
= tan
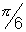
=
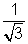
at x = 1,
f'(1) = tan
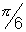
=
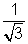
at x = 2
f'(2) = tan
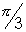
=
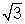
at x = 3
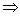
f'(3) = tan
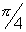
= 1
Then,
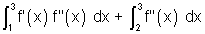
Let f'(x) = t
f''(x) dx = dt
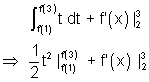
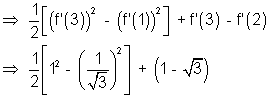
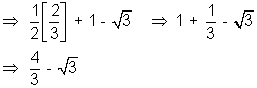 Key Words
Key Words:
* Derivative.
* TAngent.
* Normal.
* Orthogonal Curves.
* Sub Tangent.
* Sub Normal.
* Rolle's Theorem.
* Layrange's Mean Value Theorem.
* Maxima.
* Minima.
* Monotonicity.