Complex Numbers - 5
ILLUSTRATION - 9.
Find the ecentricity of elipse whose equation is |z - 4| + |z - 12⁄5| = 10 Ans:- Comparing with givem from we get
z1 = ae = 4 1st focus
z2 = be = 12⁄5 2nd focus
& 2a = 10
=> a = 5
=> ae = 4
5e = 4
=> e = 4⁄5 Ans.
1. Iota (i) is neither 0 nor greater than 0, nor less.
2. Amp(z) - Amp(-2) 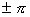 depends as amp(z) positive or negative
depends as amp(z) positive or negative
3. Segment joining points z1 & z2is divided by point z in the ratio m1 : m2 then
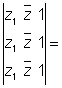 where m1 m 2
where m1 m 2  R
R
4. Three point z1, z 2, z3 collinear if  0
0
5. 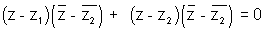 is the equation of circle with diameter AB where A ( z1) & B
is the equation of circle with diameter AB where A ( z1) & B
6. 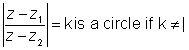 & is aline if k =
& is aline if k =
7. For evaluation (a + b)c + id we write a + ibc + id = e logea + = ec + id logea + ib
8. If avg are concyclic.
are concyclic.
ILLUSTRATION - 10.
Show that the centre of the circle whose two diametrically opposite point are z1 & z2 is 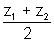
Ans. We know taht of a point z divides z1 & in ratio m : n then z =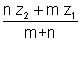
Here m = n = 1 Therefore
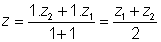
Q. 1. Find the value of 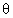 for while a real volue of x will satisfy the equation
for while a real volue of x will satisfy the equation 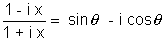
Ans:- 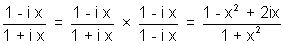
So, 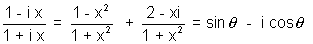
Equating real & Imaginary parts of equation 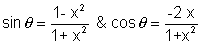
Removing x from above two equation we get 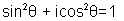 ,which is an identity & true for every
,which is an identity & true for every 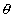 .
.
Q.2. Rind the square root of 15 + 8i.
Ans Let the square root of 15 + 8i be a + 1 Then 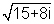 = a + bi squaring both
= a + bi squaring both
we get 15 + 8i = a2 - b2 & 8 = 2ab Solving above two equation a = 4, b = Hence square root of 15 + 8i is 4 + i
Q.3. ………… 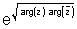
Ans If z = 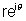
then 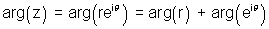
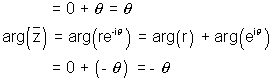
Therefore 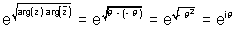
modules of ei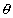 = 1
= 1
Argument of ei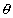 =
= 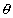
Q. 4. Find the value of 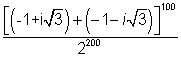
Ans:- We know that 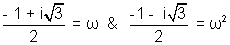
Henc 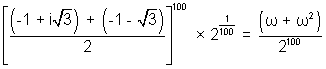
Therefore 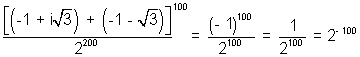
Q.5. If z1 & z2 are two complex number, then find the value of k in the equation |z1 + z2|2 = |z1|2 + |z2|2 + ki ?
Ans:- We know that,
|z1 + z2|2 = |z1|2 + |z2|2 + 2 Re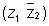
Comparing with the given form we get,
|z1|2 + |z2|2 + ki = |z1|2 + |z2|2 + 2 Re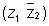
=> Ki = Real
So k should be purely Imaginary Number.
Q. 6. If iz3 + z2 - z + i = 0 . Find modulus of z.
Ans:- iz3 + z2 - z + i = 0
iz3 + z2 + i2z + i = 0
z2(iz + 1) + i(iz + 1) = 0
(z2 + i)(iz + 1) = 0
Solution are z =i & z2 = - i
Considering z = i Taking modulus on both sides
|z| = |i| = 1
Now consider z2 = -i, Take modulus of both sides
|z2| = |-i| = 1
|z2| = |z|2 = 1
=> |z| = 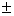 1 but |z|
1 but |z| 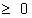 always
always
Hence |z| = 1
Q.7. ……………
number z satisfying |z - i| = 4
Ans:- We know taht |z1 -|z2| 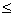 |z1-z2|
|z1-z2| 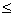 |z1-z2
|z1-z2
Here z1 & z2 = i
So |z| - |i| 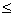 |z - i|
|z - i| 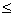 |z| + |i|
|z| + |i|
|z| - 1 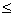 4
4 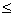 |z| + 1
|z| + 1
|z| - 1 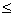 => |z|
=> |z| 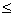 5
5
|z| + 1 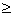 => |z|
=> |z| 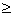 3
3
Hence 3 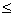 |z|
|z| 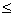 5
5
Q.8. Find the locus of z Satisfying lthe equation Arg 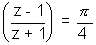
Ans:- Let z = x + iy yhen Arg 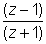 = Arg(z - 1) - Arg (z + 1)
= Arg(z - 1) - Arg (z + 1)
= Arg((x - 1) + iy) - Arg ((+ 1) + iy)
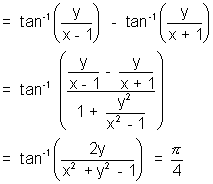
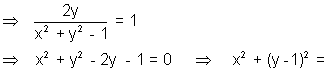
 Locus is a circle with centre(0, 1)& radius.
Locus is a circle with centre(0, 1)& radius.
Q.9. If 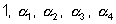 be roots of equation x5 - 1 Then find the value of
be roots of equation x5 - 1 Then find the value of
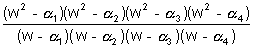
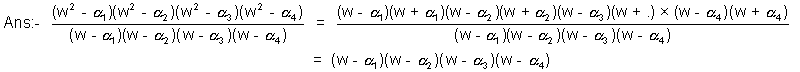
Now we know lthat
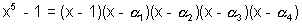
In this equation replacing x by - x we get
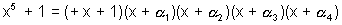
Now in this equation replacing x by we get
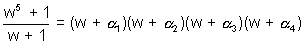
Hence the value is 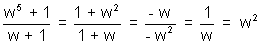
Q. 10. Find the condition so that complex numbers z1 & z2 & origin form an isosceles triangle with vwetical angle 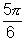 .
.
Ans:- In this case |z1| = |z2|
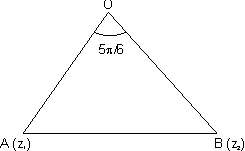
A = |z1|
B = |z2|
Applying Rotation thesrem to this trianglem takin origin at O we get
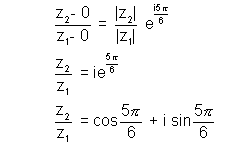
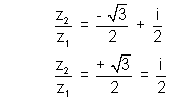
Squaring both side & rearecanging we get
z22+ z12 +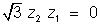
Q.11. Show that the area of the triangle of the argand digram formed by iz, -z & -z + iz is 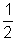 |z|2 ?
|z|2 ?
Ans:- It is clear from the vector theory that the Right angled triangle can be made through these three comples number. Area of Right angled triangle = 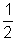 X base X height
X base X height
base = |iz| = |z|
Height = |i2z| = |-z| = |z|
Area = 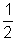 X |z| X |z| =
X |z| X |z| = 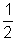 |z|2
|z|2
Dumb Question:- Why this D is a right angled ?
Ans:- Take any complex no. as z. If you multiply it with i we get iz = zeiz/2 If 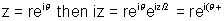 Hence iz is the complex no. having same modulus as z but amplitude is 90 more than z.
Hence iz is the complex no. having same modulus as z but amplitude is 90 more than z.
Q.1. If w is the nth root of unity & z1 & z2 are any two complex number prove that
 ( n
( n 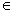 N)
N)
Ans:- If 1, w, w2, …….wn - 1are n nth roots of unity then 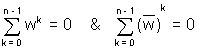
Now consider
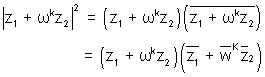
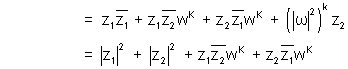
So,
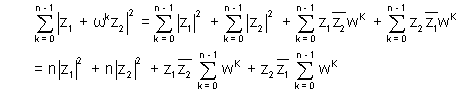
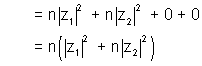
Hence proved
Dumb Question:- If 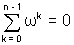 then how
then how 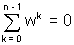 .
.
Ans:- If 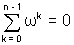 Take conjugate of both side
Take conjugate of both side

Q. 3. Prove that xy(x + y)(x2 + y2 xy) is a factor of g(x, y) = (x + y)n - xn - yn
Ans:- (xy)(x +y)(x2 + y2 + xy) can be writen as
f(x, y) = (xy)(x + y)(x - wy)(x - w2y)
If we can prove taht whenever f(x,y) = 0, g(x,y) = (x + y)n - xn - y n is also 0, then f(x,y) is always a factor of (x + y)n - xn - yn
1. Put x = 0 which is afactor of f(x,y) in g(x,y)
we get g(0, y) = (0 + y)n - 0n - yn
= yn - y n = 0
i.e. (x - 0) is a factor of g(x,y)
2. Put y = 0 whichis a factor of f(x,y) in g(x,y)
g(x, 0) = (x + 0)n - xn - 0n
= xn - xn = 0
i. e. (y - 0) is also a factor of g(x, y)
3. Put (x + y) = 0 which is a factor of f(x, y) in g(x, y)
g(x, y)/x + y = 0 = 0n - (- y)n - yn
= - (- y)n - yn (becaise n is 0
i.e (x + y) is also a factor of g(x, y)
4. Put x = wy which is afactor of f(x, y) in g(x, y)
g(wy, y) = (wy + y)n - (wy)n - yn
= yn [- w2n - wn - 1]
g(wy, y) = - yn(w2n + w + 1)
n is not a multiple of 3, n can be 3n + 1 or 3n in bot the cases w2n + wn + 1 = 0, Hence g(wy, y) = 0
i.e. (x - wy) is also a factor of g(x, y)
5. Put x = w2y which is a factor of f(x, y) in g(x, y)
g(w2y, y) = (w2y + y)n - (w2y)n - yn
= yn(- w2 - w2n - 1)
= - yn(1 + wn + w2n)
g(w2y, y) = 0
i.e. (x - w2y ) is also a factor of g(x, y) combing all the above factor which are common to both we can say xy(x + y)(x2 + xy + is a factor of g(x, y) = (x + y)n - xn - yn
Q.3. Interpret the equation geometrically on the Argand plane : 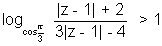
Ans:- 
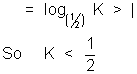
S0, 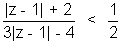
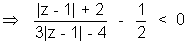
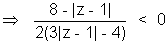 Put |z - 1| = x
Put |z - 1| = x
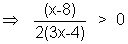
So x > 8 & x < 4⁄3
Hence |z - 1| > 8 represents th exterior of a circle with centre (1, 0) & radius 8 & |z - 1| < 4⁄3 represents the interior of a circle with centre (1, 0) & radius 4⁄3 :
Dumb Question:- Why K < 1⁄2 when log1⁄2K > 1
Ans : log1⁄2K > 1 means. log1⁄2K > log1⁄2K > 1⁄2 And we know that when the base is less than 1 the
inequality cahnges. Hence K < 1⁄2
Q.4. Diwaing f(z) by z - 2i we ge remainder i diwding by z + 2i we get the remainder 2i. Find the remainder upon division of z2 + 4 ?
Ans:- 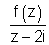 gives remainder as i means
gives remainder as i means
f(z) = K(z - 2i) + i
i.e. f(2i) = i
& f(-2i) = 2i