Complex Numbers - 6
since z2 + 4 is a quadratic expression we get a Linear remainder so
f(z) = g(z)(z 2 + 4 ) + az + b
We have f(2i) = i = 0 + 2ia + b ………………………………………… (1)
f(-2i) = 2i = 0 + (-2i)a + b …………………………………………… (2)
Solving equation (1) & (2) we get
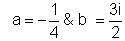
Hence the remainder is az + b
i.e. 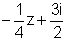
Q. 5. If z is unimodular & 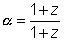 then prove that
then prove that 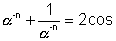 (n amp(z))
(n amp(z))
Ans:- If z is unimodular let z = 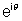
then 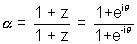
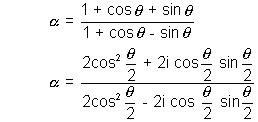
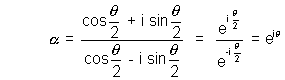
Hence 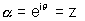
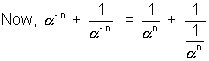
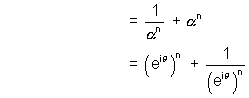
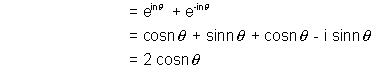
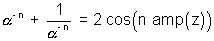
Q.6. Prove the 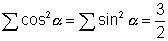 if
if 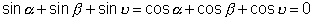
Ans:- We can write
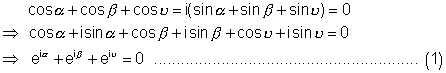
We can also
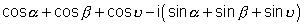
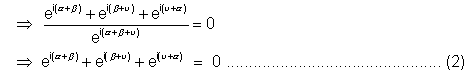
Squaring eqn. (1) we get
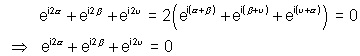
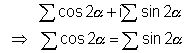
Take 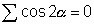
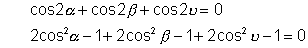
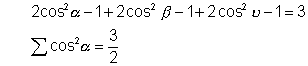
Now write 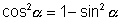 & we get
& we get 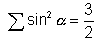
Q.1. Find all the circle which are orthogonal to |z| = 3|z - 1| = 4
Ans:-
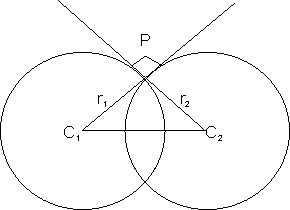
We have to find out the circles which are orthogonal to above these two circles i.e. tangents at the point of contact are at right angle to each other we know that
r12 + r22 = (C1C2)2 (Applying pythogorus Theorem in  PC1C2
PC1C2
Let the circle 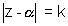 cuts orthogonally to |z| = 3 then
cuts orthogonally to |z| = 3 then
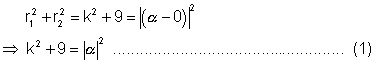
Also given that circle 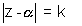 cuts |z - 1| = 4 orthogohally . so
cuts |z - 1| = 4 orthogohally . so
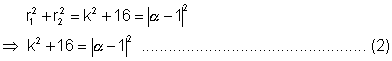
Now 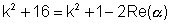
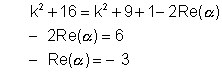
So we can write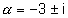 where + is any variable which corresponds to all the circles of family
where + is any variable which corresponds to all the circles of family
Hence the requred equalion for family curves is
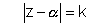
& 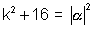
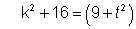
Hence K2 = t2
equation is 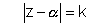
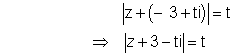
Q.2. Solve equation z14 - 1 = 0 & deduce taht
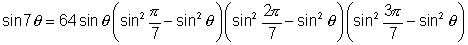
Ans:- 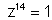
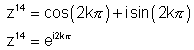
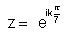 k = 0, 1, 2, ………………….. , 13 are the roots of equation.
k = 0, 1, 2, ………………….. , 13 are the roots of equation.
So roots are 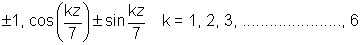
Hence we can write
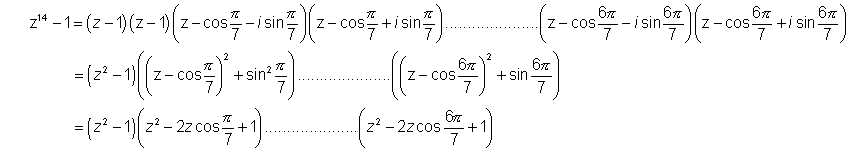
Diuiding both sides by z we get
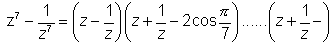
Now put 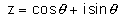
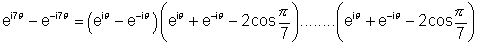
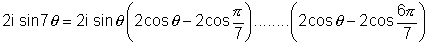
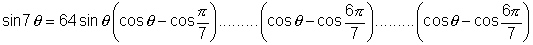
We know that 
If 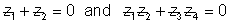 the prove the points representing 4 complex number
the prove the points representing 4 complex number 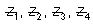 in Argand plane are concyclic .
in Argand plane are concyclic .
Ans:- Let 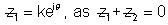
We get 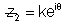
Let 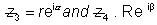
Now 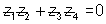
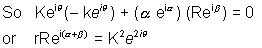

Squaring and adding, rR K2 …………………………………………… (1)
Dividing, we get,
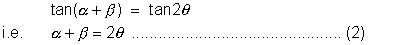
Let equation of circle passing through 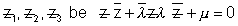
Now , 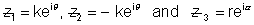 satisfy the equation.
satisfy the equation.
So, we have,
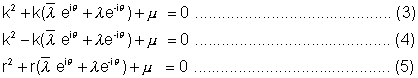
Adding (3) and (4),we get
s And therefore,
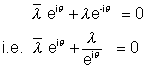
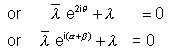
(By using (2))

Taking conjugate , we get

By adding (7) and (8) we get
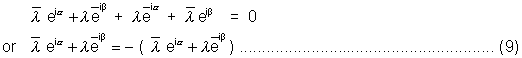
Put these values in (5) to get
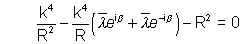
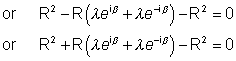
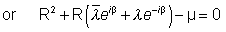 (from (6))
(from (6))
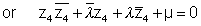
Thus 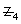 also satisfies the equation of circle.
also satisfies the equation of circle.
Hence the problem.
Dumb Question:- How can we assure that circle 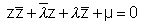 passes through
passes through 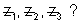
Ans:- Well when three pointin a plane are given a unique circle passing through those 3 point can be trawn and here
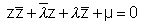 is that circle only.
is that circle only.
- Iota, i
- Imaginary Part
- Real Part
- Complex Number
- Argand Plane
- Real axis
- Imaginary axis
- Conjugate
- Modules
- Argument
- Principal Argument
- De - movier’s Theorem
- nth root of unity
- Rotation Theorem
- w. cube root of unity
- Amplitude
