Electromagnetic Induction - 1
Electromagnetic Induction
Intoduction
One of the most important concept ever given in the field of electricity and magnetism is the concept of ELECTROMAGNETIC INDUCTION. This was the first law which combinedd both fields electricity and magnetism. It worked the begining of a new era which followed the discovery of various principles and laws. MAGNETIC FLUX:
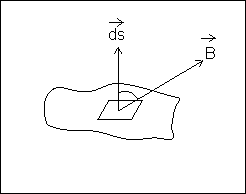
The magnetic flux experents total magnetic lines of forces passing through a given area. If the magnetic field at an element as shown in the adjoining figure is
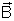 , the magnetic flux through the element is:
, the magnetic flux through the element is: 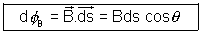
Here
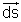 = Perpendicular vector to the surface and has a magnitude equal to the area ds.
= Perpendicular vector to the surface and has a magnitude equal to the area ds.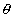 = Angle between
= Angle between 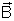 and
and 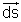 at that element.
at that element.Thus, total magnetic flux through the =
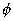 B =
B = 
Surface is the sum of the contributions from the individual area elements =
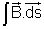
Dumb Question: What are manetic field lines ? How they differ from electric field lines?
Ans: We can represent any magnetic field by Magnetic Field lines. The idea of magnetic field lines is same as for the electric field lines.
The magnetic field at any point is longential to the field line at that point where the field lines are close, the magnitude of field is large, where the field lines are for apart, the field magnitude is small.
Similarly, as electric field lines magnetic field lines but never intersect each other maintaining the field that the direction of
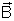 is unique at every point.
is unique at every point.But, unlike the electric field lines magnetic lines from a closed lup.
Dumb Question: What is the direction of area vector
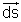 ?
?Ans:

As a rule remember that direction of area vector
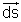 is always taken to be the Outward Normal to the surface on which the flux is to be caculated. As per example in te adjoining figure suppose we have to find flux on the surface. At this time directions of normal at AB are possible given by
is always taken to be the Outward Normal to the surface on which the flux is to be caculated. As per example in te adjoining figure suppose we have to find flux on the surface. At this time directions of normal at AB are possible given by 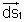 and
and 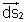 . Now, outward normal is
. Now, outward normal is 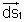 so, we will take it. Similarly the outward normal to surface at CD is
so, we will take it. Similarly the outward normal to surface at CD is 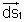 and not
and not 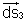 .
.FARADAYS LAWS:
On changing the magnetic flux through a loop, an electromotic force (e.m.f.) i.e. induced in the loop which lasts as long as the magnetic flux keeps on changing. The magnitude of this e.m.f. is equal to the negative rate of change of flux, that is,
Induced e.m.f. = E =
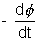
where
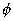 = N
= N 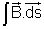
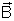 = Magnetic Induction.
= Magnetic Induction.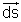 = Area element.
= Area element.N = Number of turns of loop.
Thus, if the resistance of the loop is R then current through it will be given by:
Iinduced =
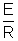
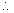 Iinduced = - Iinduced = - 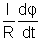 |
Direction of Induced E.M.F.
The steps to decide the direction are:
(1) Define a positive direction for the area vector
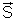 .
.(2) From the directions of
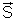 and the magnetic field
and the magnetic field 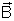 , determine the sign of
, determine the sign of 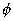 B and its rate of change
B and its rate of change 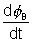 .
.(3) Determine the sign of the induced current. If
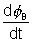 is positive, that is, flux is inerseasing, sign of induced current is negative and ……
is positive, that is, flux is inerseasing, sign of induced current is negative and ……(4) Finally determine the direction of induced current using your right hand. Curl the fiugers of your right hand around
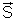 , with your thumb in the direction of
, with your thumb in the direction of 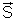 . If the induced current is positive, it is in the same direction as your curled fiugers and if it is negative it is in the opposite direction.
. If the induced current is positive, it is in the same direction as your curled fiugers and if it is negative it is in the opposite direction.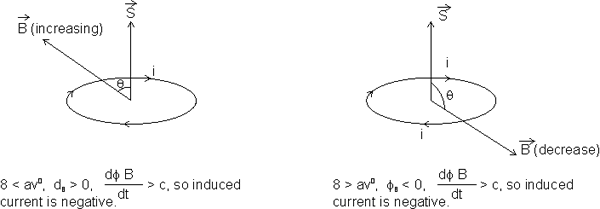
Illustration 1: A circular loop of radius r having N turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown inthe figure. Find the e.m.f. induced as in loop if it is rotate with a uniform angular velocity w about.
(a) An axis passing through the centre and perpendicular to the plane of the loop.
(b) a diameter ?
Ans: (a) The e.m.f. is inuced when there is change of flux. But, in this cuse there is no change of flux have no e.m.f. will be induced.
(b) If the loop is rotated about a diameter there will be change of flux with time, in this case e.m.f. will be induced in the coil.
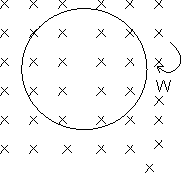
The area of the loop is A = 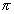 r2. If the normal of the loop makis an angle
r2. If the normal of the loop makis an angle 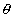 = 0 with the magnetic field at t = 0, this angle will become
= 0 with the magnetic field at t = 0, this angle will become 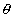 = wt at time t.
= wt at time t.
The flux of magnetic field at this tim is 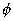 = nB
= nB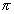 r2 cos
r2 cos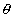
= nB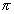 r2 coswt
r2 coswt
The induced e.m.f. is
E = 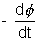
= 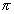 nr2Bw sinwt.
nr2Bw sinwt.