Functions:
Sketch of curve y = sec(sec-1x):
Domain

R - (-1, 1)
& range y = x
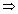
y

R - (-1, 1)
y = sec(sec
-1x) = x, only when x

(-
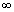
, -1)
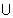
(1,
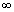
)
Sketch of y = cot(cot-1x):
Domain

R - (-1, 1)
& range y = x
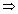
y = R
We should sketch
y = cot(cot
-1x) = x
v x

R
Sketch of y = sin-1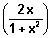
:
Domain [-1, 1]
v x

R
& range y

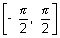
b/c y = sin
-1
y

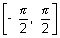 Dumb Question
Dumb Question: How domain is [-1, 1]
v x

R ?
Ans:
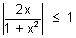
i.e.
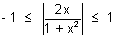
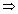
2|x|
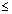
1 + x
2 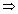
|x|
2 - 2|x| + 1
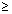
0
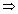
(|x| - 1)
2 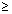
0
x

R
Let x = tan
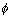
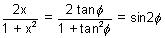
y = sin
-1(sin2
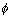
) =
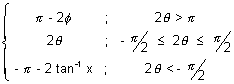
This curve has sharp edge at x = ± 1
So, not differentiable at x = ± 1
Dumb Question: How does y =
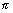
- 2

for 2

>
Ans: Since our y

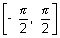
. So, if 2

>
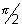
to make it we substract it from
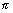
- 2

because sin(
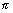
- 2

) = sin2
 Sketch of y = cos-1
Sketch of y = cos-1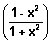
For domain
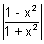
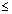
1
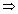
|1 - x
2|
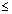
1 + x
2
Which is true for all n; as 1 + x
2 > 1 - x
2 x

R
domain

[-1, 1]
For range
y =cos
-1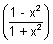
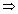
y

(0,
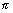
)
Let x = tan

y = cos
-1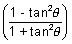
= cos
-1(cos2

)
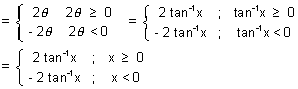 Dumb Question
Dumb Question: How cos
-1(cos2

) = - 2 tan
-1x when x < 0 or

< 0
Ans: Range of y

[0,
]. So, when

< 0 or x < 0
Then we have to make it b/w [0,
]
So, cos
-1(cos2

) = - 2

when

< 0
because
cos(- 2 ) = cos2 ) = cos2 |
This curve has sharp edge at x = 0. So, not differentiable at x = 0.
Sketch of y = tan-1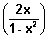
For domain
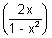

R except 1 - x
2 = 0
i.e. x
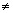
± 1
or x

R - {1, -1}
domain

R
Range y = tan
-1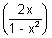
as y = tan
-1
y

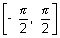
Let x = tan

y = tan
-1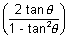
= tan
-1(tan2

) =
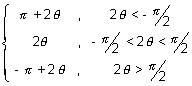
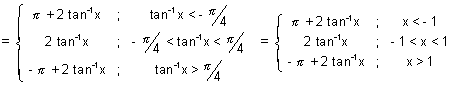 Dumb Question
Dumb Question: Why y = tan
-1(tan2

) = -
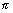
+ 2 tan
-1x, for

>
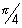
?
Ans: Range of y

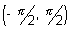
& when

>
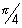
So, 2

>
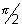
.
To make it within range we substract
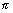
So, it comes under range.
Because of tan(-
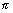
+ 2

) = tan2

, this can be done.
This curve is neither continous nor differentiable at x = {-1, 1}
Sketch of curve y = tan-1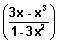
For domain,
y = tan
-1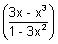
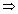
x

r except 1 - 3x
2 = 0
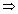
x
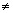
±
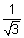
x

R - {±
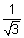
}
domain

R
For range
y = tan
-1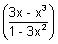
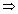
y

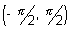
Let x = tan

y = tan
-1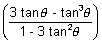
= tan
-1(tan3

) =
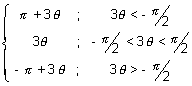
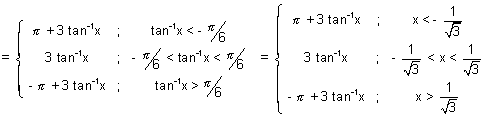 Dumb Question
Dumb Question: Why tan
-1(tan3

) =
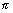
+ 3

if

< -
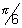
?
Ans: Range of tan
-1(tan3

) is
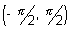
but if

< -
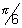
So, 3

< -
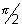
So, to make it within given range. We add
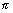
to it.
and in III
rd quadrant.
tan(
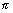
+ 3

) = tan3

So, this is done.
This curve is neither cont. nor differentiable at x = ±
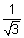
.
Sketch of y = sin-1(3x - 4x3):
For domain
y = sin
-1(3x - 4x
3)
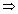
x

[-1, 1]
For range
y = sin
-1(3x - 4x
3)
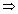
y

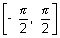
Let x = sin

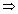
y = sin
-1(sin3

) =
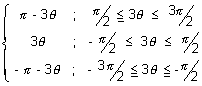
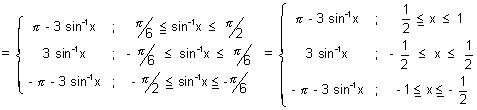
This curve has sharp edge at x = ± 1/2 so, not differentiable at x = ± 1/2.