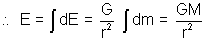For making a body revolve, a centripetal force is required. In case of earth-sun system there exists a new type of force called ‘gravitational force’ which is responsible for it. This force is always attractive in nature. In this unit we will study in detail about this force and also calculate the velocities with which a body must be projected from earth’s surface. So that it never comes back to earth surface.
NEWTONS LAW OF GRAVITATION:
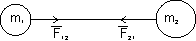
It states that every particle in the universe attracts every other particle with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Force is direct along the line joining the particles and towards other particle.

whre G => Universal gravitational constant.

=> Unit vector joining two particles.
° The gravitational force between two particles form an action reaction pair.
° If we consider a system which has both boies as its constituents then the net force becomes zero

.
° The magnitude of the forces acting is same on both bodies but direction is opposite.
Dumb Question: What if more than two particles are present.
Ans: In that case the principle of super position can be applied for summing the forces.
Illustration: Find the gravitational force of attraction on the point mass ’m’ placed at O by a thin rod of mass M and length L as shown in figure.
Solution: First we need to find the force due to an element of length dx. The mass of the element is dm =
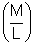
dx.
So, dF =

The net gravitational force is
F =
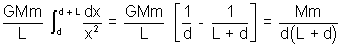
Notice that when d >> L, we find F =
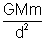
, the result for two point masses.
GRAVIATTIONAL FIELD:
Gravitation field is due to mass. It is defined as the region of space in which it interacts with other masses. Another relevent quantity is gravitational field intensity.
° GRAVITATIONAL FIELD INTENSITY due to a mass ’m’ at a distance ‘r’ is defined as the force acting on unit mass kept at a distance r. It is a vector quantity and its direction is the direction along which te unit mass has tendency to move.
Few gravitational fields :
| ° Due to a point mass |
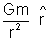 |
| ° Due to ring at an axial distance |
 |
| ° Field due to disk |
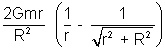 |
| ° Due to thin spherical shell |
inside = 0
outside = 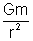 |
| ° Field due to solid sphere |
inside = 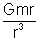
outside = 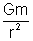 |
Why ??
Intensity due to a uniform circular ring at a point on its axis:
Figure shows a ring of mass M and radius. Let P is the point at a distance r from the center that is along
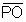
.
From the figure, AP =

Now field at P due to dm along
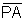
has magnitude = dE =
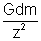
dE
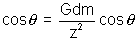
Net Gravitational field E =
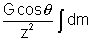
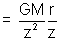
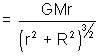
dry
 Dumb Question
Dumb Question: As the P is moved for away, how will the intensity change ?
Ans: for r >> R, r
2 + R
2 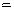
r
2

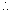
field varies inversely to the square of distance
however if r << R, r
2 + R
2 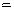
R
2
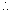
E = -
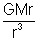
or E
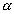
r ,
for very close distances, field varies directly with r.
•
Intensity due to a uniform disc at a point on its axis:
Let mass of disc be M and radius be R and P be pt. m its axis where gravitational field is to be calculated.
Taking a small ring of thickness dx and radius x in the disc.
Man of the ring dm =
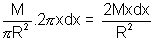
field at P due to ring is
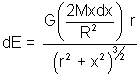
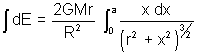
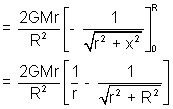
in term of
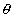
E
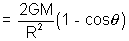
•
Field due to a solid sphere:
Let the mass of sphere is M and its radius is R,
Case I:
External point
Choosing a thin shell of mass dm
then dE =
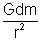
[for a point outside hollow shell, it acts as a point mass … at centre of shell]