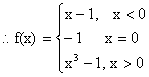limit-continuity-4
L’ Hospital’s Rule:
L’ Hospital’s Rule is applied only to the two forms ![]() .The rule states that if
.The rule states that if ![]() is of the form
is of the form ![]() then
then ![]() provided later limit exists. But if still it takes the form
provided later limit exists. But if still it takes the form ![]() then we differentiate numerator and denominator again.
then we differentiate numerator and denominator again.
i.e. ![]() and this process continues till we find that
and this process continues till we find that ![]() form is removed.
form is removed.
Illustration 13:
Evaluate ![]()
Solution:
Let A = ![]()

Continuity at point:
A function ‘f’ is said to be continuous at a point ‘a’ in domain of f, if following conditions are met.
1) f (a) exists.
2) ![]() exists finitely which essentially means that
exists finitely which essentially means that ![]() and
and ![]() both exist finitely and are equal.
both exist finitely and are equal.
3) ![]() . If anyone or more conditions are not met than function f is said to be discontinuous at point ‘a’. Geometrically graph of function exhibit a break at point x=a.
. If anyone or more conditions are not met than function f is said to be discontinuous at point ‘a’. Geometrically graph of function exhibit a break at point x=a.
Illustration 14: Discuss the continuity of function y = f(x) as shown by graph below at the point x=1.
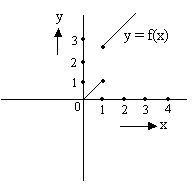
Fig (3)
Solution:
Now clearly the function exhibits a break at point x=1 and is thus discontinuous at x=1. But if we go by the rules mentioned in above article we observe that.
![]() And
And ![]()
So ![]() does not exists and thus the function is discontinuous at x=1.
does not exists and thus the function is discontinuous at x=1.
Continuity of function in open interval:
A function f is said to be continuous in (a, b) if f is continuous at each and every point belonging to interval (a, b).
Continuity of function in closed interval:
A function f is said to be continuous in closed interval [a, b] if
1) f is continuous in open interval (a, b) and
2) ![]() exists finitely and
exists finitely and ![]() and
and
3) ![]() exists finitely and
exists finitely and ![]() .
.
Illustration 15:
Consider a function f(x) which is continuous in [1, 2] and given that f (1) = -1 and f (1) = 2, prove that there exists a point x such that f(x) =1.
Solution:
Let us arbitrarily choose some graph for f(x)
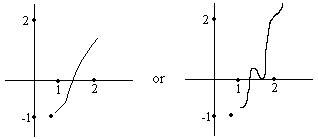
Fig (4)
For that matter function f(x) can take any shape. But since the function f is continuous between 1 and 2 it must be defined on all values lying between 1 and 2 and the function’s curve will go from y = -1 to y = 2 through some path. Whatever path be chosen y =1 will lie in between (Remember there cannot be a sudden jump because function is continuous)
Hence there exists a point x-where f(x) = 1.
Properties of continuous functions:
Let f(x) and g(x) are continuous functions at x=a then
1) K f(x) is continuous where K is constant
2) f(x) ± g(x) is continuous at x=a.
3) f(x) ´g(x) is continuous at x=a.
4) f(x)/g(x) is continuous at x=0 provided g (a) ¹ 0.
5) If m = f(x) is continuous at x=x0 and f (m) is continuous at the point m0 = f(x0), then composite function f (f(x)) is continuous at point x0.
6) If f(x) is continuous on [a, b] such that f (a) and f (b) are of opposite signs. Then there exists at least one solution of equation f(x) = 0 in the open interval (a, b).
7) Functions like sinx, cosx, tanx, cotx, secx, cosecx, logx, ex etc are continuous in their domain.
Dumb Question:
1) How can function like tanx be continuous?
Ans: Please read the point mentioned above carefully. It is written that tanx is continuous in its domain. The points (2n+1)p/2 when tanx®![]() do not lie in the domain of function f.
do not lie in the domain of function f.
Illustration 16:
Let function ![]() Prove that there is a solution for equation f(x) =0 in the interval [0, 1].
Prove that there is a solution for equation f(x) =0 in the interval [0, 1].
Solution:
We observe that ex, cosx, sinx, ![]() all are continuous functions in interval [0, 1]. So the function f is also continuous in [0, 1].
all are continuous functions in interval [0, 1]. So the function f is also continuous in [0, 1].
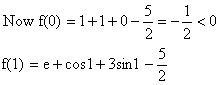
Since 0<1< (p/2) so cos1 and sin1 are positive quantities and e> ![]() .
.
So, f (1)>0.
Now f (0) and f (1) are of opposite signs. So f(x) =0 has a solution in interval [0, 1].
Classification of discontinuities:
1) Removable discontinuity:
Here at a point x=a of discontinuity, ![]() exists but f (a) is either undefined or if defined it does not tally with
exists but f (a) is either undefined or if defined it does not tally with ![]() .
.
In this case the removal of discontinuity is achieved by modifying definition of function suitably so that f (a) tallies with ![]() which is found existing.
which is found existing.
2) Irremovable discontinuity:
Here ![]() does not exist even though f (a) exists or additionally f (a) also does not exist.
does not exist even though f (a) exists or additionally f (a) also does not exist.
Here, since ![]() does not exist, no modification of definition at x=a can succeed to make
does not exist, no modification of definition at x=a can succeed to make ![]() exist. Hence discontinuity remains irremovable.
exist. Hence discontinuity remains irremovable.
Illustration 17:
Consider the function
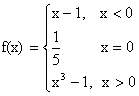
Discuss the continuity of function at x=0. If discontinuous suggest how to remove discontinuity.
Solution:
Let us plot the function f(x)
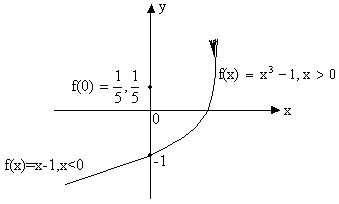
Fig (5)
Now ![]()
And ![]()
So, ![]() =
= ![]() = -1
= -1
But f (0) = ![]() .
.
\f (x) has removable discontinuity and f(x) can be made continuous by taking f (0) = -1.