study material-mathematics-algebra-logarithms
Logarithms - 1
Definition:-
We define log as, ay = x than y = logax. in logax. both x and a are positive ie. x > 0 and a > 0 and also a 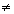 1.
1.
Dumb Question:- Why a cannot be 1 ?
Ans:- Suppose a is 1 then let us attempt to y such that y = log1x.
Now according to definition of log.
1y = x.
But no matter what power we raise to 1 the answer will be. 1 only so we will never never be able to find y.
Hence a cannot be 1.
Some important formulae:- (Formulaes marked with * are important. This is not be printed)
- logaa = 1.
- logany1 = 0.
- logca = logba.logcb.
Why ?
Let logba = x and logcb = y
So, by definition, a = bx ………………………………. (i)
b = cy ……………………………….. (ii)
Using (i) & (ii) a = cxy
Now taking log on both sides.
logca = xy
logba.logcb.
Illustration - 1.
Find value of log210.log102 ?
Using formula 3 we get.
log210.log102 = log1010
Now using formula 1 we get
log1010 = 1
Hence log210.log102 = 1
- loga(m.n) = logam + logan
Why ?
Let logam = x
logan = y
So, m = ax and n = ay [Using definition]
m.n = ax.ay = ax + y
=> loga(mn) = logaax + y
= x + y
= logam + logan.