study material-mathematics-algebra-matrices
Matrices & Determinants - 8
M 2. Using elementary row trans formations find the inverse of the matrix A = 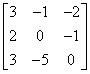
Soln :- A = I A
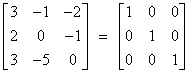 A
A
. R1![]() R1 - R2
R1 - R2
. R2 ![]() - 2R1 and R3
- 2R1 and R3 ![]() R3 - 3R1
R3 - 3R1
. R2 ![]() 1⁄2 R2
1⁄2 R2
. R1 ![]() R1 + R1 and R3
R1 + R1 and R3![]() R3 + 2R2
R3 + 2R2
. R3 ![]() 1⁄2 R3 and .R1
1⁄2 R3 and .R1![]() R1 + 1⁄2 R3 and R2
R1 + 1⁄2 R3 and R2![]() R2 - 1⁄2 R3
R2 - 1⁄2 R3
We get :-
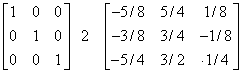 A
A
A -1 = 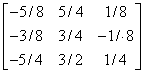
M 3 If a, b and c are Pth1 qth and rth terms of are
H.P., prove taht 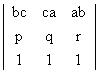 = 0
= 0
Solution :- A : First term, D : Common difference
1/a = A +(p -1) D, 1/b = A +(q - 1) D, 1/c = A + (r - 1)D
 abc
abc 
R1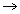 R1 - D R2 - (A - D)r ,
R1 - D R2 - (A - D)r ,
 = abc
= abc 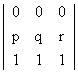 = 0
= 0
M 4 . for what valume of m, does the system of equation 3x + my - mand 2x - 5y = 20 lhas a solution satisfying the condstion. x > 0, y > 0.
Solution  =
= 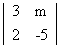 = - (15 + 2m)
= - (15 + 2m)
 1 = - 25m
1 = - 25m  2 = 60 - 2m
2 = 60 - 2m
X = 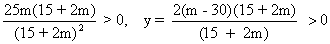
=> m > 30 or m < -15⁄2