Sequence and Series is one of the most important chapter that is covered in the syllabus for IIT-JEE. The summation of series is one of the most important way to reduce large series into some value and it is widely used throughout the syllabus. The tricks and techniques discussed here are very useful and are widely used in other chapters as well. The A.M- G.M inequality which will be discussed here is also a very important result that is used widely.
So Let us Probe more into this Chapter...
Arithmetic Progression (A.P):
A sequence of numbers is said to be in A.P when difference 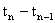 is constant for all
is constant for all
n
Î N. This constant

is called common difference. If a the first term and d the common difference of the A.P then,
1) nth term tn = a+ (n-1) d.
Proof
1st term of A.P = a = a+ (1-1) d.
2nd term of A.P = a+d = a+ (2-1) d.
3rd term of A.P = a+2d = a + (3-1) d.
4th term of A.P = a+3d = a + (4-1) d.
\ nth term of A.P = a + (n-1) d.
2) Sum of n terms

Why?
Let Sn = a + (a+d) + (a+2d) + ------- + a+ (n-2) d + a+ (n-1) d --------- (1)
Or Sn = a+ (n-1) d + a+ (n-2) d + ------------ + (a+d) + a ---------- (2)
Now adding (1) and (2) we get
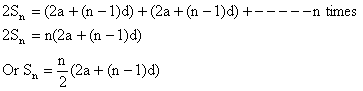
Arithmetic Means (A.M):
The n number A1, A2, A3---------, An are arithmetic means between a and b if a, A1, A2, -----An, b are in A.P.
Since a is first term and b is (n+2) th term.

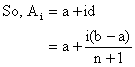
Note:
1) 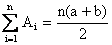
Why?

2) Arithmetic mean A of n numbers a1, a2, ----------- an is given by,
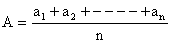
Illustration 1:
For what value of n 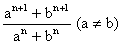 is A.M between a and b?
is A.M between a and b?
A.M between a and b is 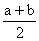
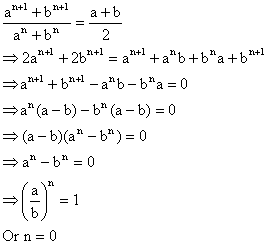
Properties of A.P:
1) If a fixed number is added (substracted) to each term of a given A.P. then resulting sequence is also A.P with same common difference as given A.P.
Dumb Question:
1) Why common difference has not changed?
Ans: Suppose the original A.P had 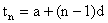 , now let g be substracted from each term. So
, now let g be substracted from each term. So 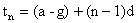 . Therefore only the first term of A.P has changed.
. Therefore only the first term of A.P has changed.
2) If each term of an A.P is multiplied (or divided) by fixed constant then resulting sequence is also an A.P with common difference multiplied (or divided) by same constant.
3) Sum and difference of corresponding terms of two A.P’s will form an A.P.
Why?
Let first A.P be
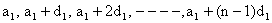
And second A.P be
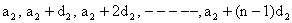
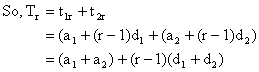
So, resulting sequence is A.P with first term a1+a2 and common difference d1+d2.
4) If we want to pick terms of an A.P then convenient way of doing that is,
For three term’s in A.P we choose a-d, a, a+d.
For four terms in A.P we choose a-3d, a-d, a+d, a+3d.
5) 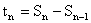
6) If a, b, c are in A.P Þ 2b = a+c or b-a = c-b.
7) The sum of the terms of an A.P equidistant from beginning and end is constant and equal to sum of first and last term.
 = Constant =
= Constant = 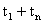 .
.
Illustration 2:
Find the number of terms in the series  of which the sum is 300.
of which the sum is 300.
Solution:
Here we observe that a=20, 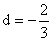 , and Sn = 300.
, and Sn = 300.
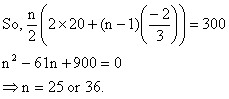
Dumb Question:
1) Why do we get n as 25 and 36 both?
Ans: This clearly indicates that sum of terms from n = 26 to 36 is zero.
i.e. 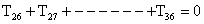
Geometric Progression:
A sequence is a G.P when its first term is non-zero and each of its succeeding term is r times the preceding term. The fixed term r is known as common ratio of G.P.
If a is first term of an G.P and r its common ratio then,
1) nth term 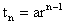 .
.
Why?
Let us observe the pattern
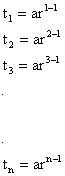
So, clearly 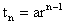 .
.
2) The sum of first n terms

Why?
Case 1: Suppose r=1
So, 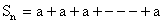
= na
Case 2: If r ¹ 1.
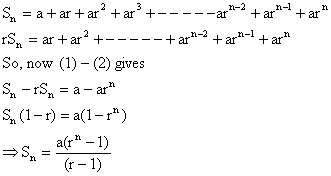
3) If |r|<1 and n® ¥ then 
Why?

Dumb Question:
1) Why 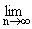 rn=0?
rn=0?
Ans: Here |r|<1 so as we multiply r by itself so the value goes down and down. For example. Suppose r = ½, so r2=1/4 is less than ½ and so the value keeps going down.
Illustration 3:
If a1, a2, a3 are 3 consecutive terms of a G.P with common ratio k and a1<0. Find values of k for which a3> 4a2-3a1 is satisfied.
Solution:
Now since a1, a2, a3 are in G.P
So a2 = a1k.
a3 = a1k2.
\ a1k2 > 4a1k-3a1.
Þ a1 (k2-4k+3) > 0.
Or a1 (k-1) (k-3) > 0.
Since a1<0 so it means (k-1) (k-3) < 0.
Þ 1<k<3.
Geometric Means (G.M)
If G1, G2, G3, G4---------Gn are in G.M’s between a and b then a, G1, G2, ----------- Gn, b are in G.P.
Now b is tn+2 so b = arn+1
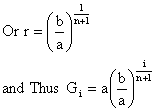
Note:
1) The product of n G.M’s between a and b is equal to nth power of one G.M between a and b
i.e. G1, G2------- Gn = 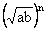 .
.
Why?

2) If a1, a2, ------- an are n non-zero numbers then their G.M is given by
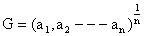
Illustration 4:
If we insert odd number (2n+1) G.M’s between 4 and 2916 then find the value of (n+1) th G.M?
Solution:
Now 4, G1, G2, G3----------- Gn+1, ------- G2n, G2n+1, 2916 are in G.P. So Gn+1 will be the middle mean of (2n+1) odd means and so it will be equidistant from 1st and last term.
So, 4, Gn+1, 2916 are also in G.P.
And thus,

= 108.
Properties of G.P:
1) If each term of a G.P is multiplied (or divided) by some non-zero quantity the resulting progression is G.P with some common ratio.
Why?
Suppose the G.P is with 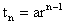
Now this G.P is multiplied by some k (¹0).
So G.P will be 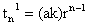
So, only the first term of G.P has changed and the common ratio remains unaffected.
2) If a1, a2, -------- and b1, b2, ---------- be two G.P’s of common ratio r1 and r2 respectively, then a1b1, a2b2, ------ and 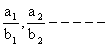 will also form G.P common ratio will be r1r2 and
will also form G.P common ratio will be r1r2 and 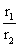 respectively.
respectively.
Why?
Let the series a1, a2--------- have the nth term as 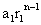 and the series b1, b2-------- have nth term as
and the series b1, b2-------- have nth term as  .
.
So the series a1b1, a2b2 ------- will have nth term as
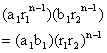
So the common ratio now becomes r1r2.
3) If we have to take three terms in G.P we take them as 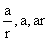 with common ratio r and four terms as
with common ratio r and four terms as 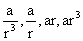 with common ratio r2.
with common ratio r2.
4) If a, b, c are in G.P then b2 = ac.
5) If a1, a2, a3 -------- an is a G.P then loga1, loga2--------- logan is an A.P.
Why?
Now a1, a2, a3 ------- an form a G.P.
So 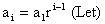
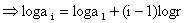
This is clearly term of an A.P.
Dumb Question:
1) How does loga1 + (i-1) logr represents term of an A.P?
Ans: Let loga1 = A
And logr = D
So, loga1+ (i-1) logr = A+ (i-1) D.
So, A+ (i-1) D is term of an A.P with first term as A and common difference as D.