Progression - 2
Illustration 5:
If x = 1+ a+ a2+a3+ --------+¥ and y = 1+b+b2+ b3+ ------ +¥ Show that,
![]()
Where 0<a<1 and 0<b<1.
Solution:
Given x = 1+ a+ a2+a3+ --------+¥
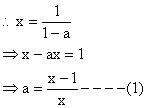
y = 1+b+b2+ b3 ------ +¥
![]()
Since 0<a<1, 0<b<1
\ 0<ab<1.
Now ![]()
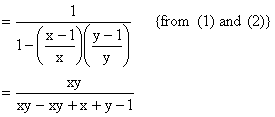
![]()
Arithmetic Geometric Series (A.G.P):
Suppose a1, a2, a3, ------- an be an A.P and b1, b2, b3, ------- bn is a G.P Then the sequence a1b1, a2b2, -------- anbn is A.G.P.
A.G.P is of form ![]()
Where clearly ![]()
1) Sum of n terms of an A.G.P
![]()
Why?
Let ![]()
Now if we multiply the series by r then.
![]()
So on substraction,
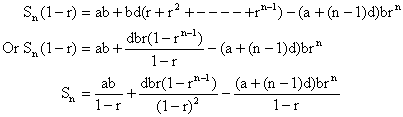
2) Sum of infinite series S¥.
![]()
Why?
If |r|<1 then ![]()
So, ![]()
Illustration 6:
If sum to infinity of the series ![]() then find x.
then find x.
Solution:
We know that ![]()
Here a=1, b=1, r=x, d = 3
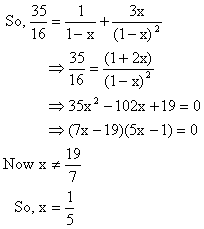
Dumb Question:
1) Why ![]() ?
?
Ans: For infinite series to be summable |x| needs to be less than 1 hence ![]()
Harmonic Progression (H .P):
The sequence a1, a2, ------ an is said to be a H.P if ![]() is an A.P.
is an A.P.
The nth term of a H.P (tn) is given by ![]() .
.
Harmonic Means (H .M):
If H1, H2, H3-------- Hn be n H.M’s between a and b then a, H1, H2, H3-------- Hn, b is a H.P.
This means ![]() is a A.P.
is a A.P.
And hence ![]()
Note:
1) If a1, a2, a3---------an are n non-zero numbers then H.M(H) of these number is given by
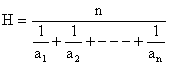
2) If a, b, c are in H.P then ![]()
Why?
a, b, c are in H.P so, ![]() are in A.P
are in A.P
And hence ![]()
Illustration 7:
If the (m+1)th, (n+1)th and (r+1)th term of an A.P are in G.P m, n, r are in H.P, Show that ratio of the common difference to the first term in the A.P is (-2/n).
Solution:
Let ‘a’ be the first term and ‘d’ be common difference of the A.P. Let x, y, z be the (m+1)th, (n+1)th and (r+1)th term of the A.P then x = a+md, y = a+nd, z = a+rd. Since x, y, z are in G.P.
\ y2 = xz i.e. (a+nd)2 = (a+rd) (a+md)
![]()
Now m, n, r in H.P

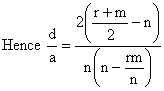
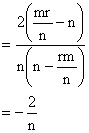
Some Important Theorems:
If A, G, H are respectively AM, GM, HM between two positive unequal quantities then.
1) A>G>H
Why?
First of all let us Prove A>G.
The two numbers be x, y.
![]()
So to prove ![]()

Hence A>G -------- (1)
Now Let us Prove G>H
Again ![]()

Combining (1) and (2) we get A>G>H.
Why G2=AH?
Let x, y be two numbers.
So, ![]()
Hence
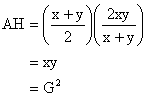
Illustration 8:
If a, b, c, d, be four distinct positive quantities in H.P then show that a+d>b+c.
Solution:
a, b, c, d are in H.P
Then A.M > H.M
For first three terms ![]()
Þ a+c>2b ------ (1)
And for last three terms
![]()
Þ b+d > 2c ------ (2)
From (1) and (2)
a+c+b+d > 2b+2c
Þ a+d > b+c.