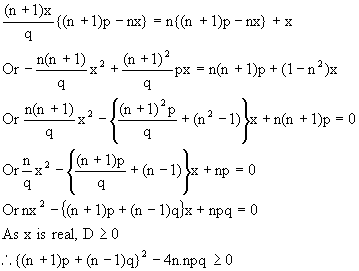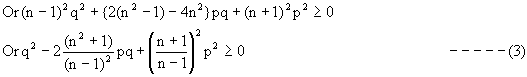Quadratic Equation - 5
Medium
Q-1: Prove that ![]() has no integral solution
has no integral solution
Solution: Let ![]() then the equation is
then the equation is ![]()
As u, v are integers, >1402
But 372 = 1369, 382 = 1444
![]() Minimum possible value of v=38.
Minimum possible value of v=38.
Also
![]() v must be even.
v must be even.
Let v=38+2k where k ![]() N
N
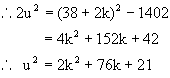
![]()
Hence D=0
i.e. ![]() which is incorrect.
which is incorrect.
![]() u, v cannot have positive integral solutions.
u, v cannot have positive integral solutions.
So, x, y cannot have integral solutions.
Q-2: If a, b are the roots of and also of ![]() and if
and if 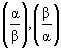 are the roots of
are the roots of ![]() then prove that n must be even integer
then prove that n must be even integer
Solution:![]()
Sincea, b are the roots of ![]()
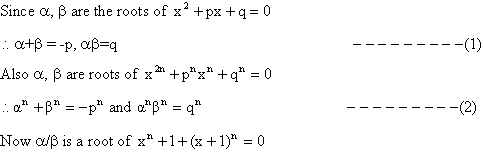

This is true only if n is an even integer.
Q-3: Show that the equation
![]() has no imaginary roots,
has no imaginary roots,
Where A, B, C---------K, a, b, c------k and l are real.
Solution: Assume a+ib is an imaginary root of the given equation then conjugate of this root a-ib is also root of this equation.
Putting x = a+ib and x = a-ib in the given equation then,
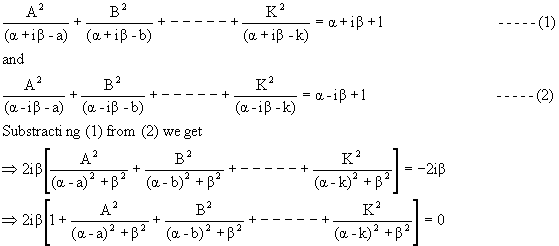
The expression in bracket ![]() 0
0
![]() 2ib = 0
2ib = 0 ![]() b = 0 (because i
b = 0 (because i ![]() 0)
0)
Hence all roots of the given equation are real.
Q-4: Solve in ![]()
Solution:
The A.M of x+3, x-1 is ![]() , i.e. (x+1)
, i.e. (x+1)
Put x+1 = y then x+3 = y+2, x-1 = y-2
![]() The equation becomes
The equation becomes ![]()
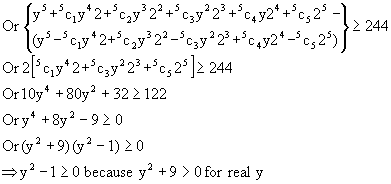
The corresponding equation =0 has roots 1, -1.
The sign scheme of y ![]() R is as follows.
R is as follows.
Fig (13)
![]() y2-1,
y2-1, ![]() 0 holds if y
0 holds if y ![]() -1 or y
-1 or y ![]() 1
1
Now y ![]() -1
-1 ![]() x+1
x+1 ![]() -1 or x
-1 or x ![]() -2
-2
y ![]() 1
1 ![]() x+1
x+1 ![]() 1 or x
1 or x ![]() 0
0
Hence x ![]() -2 or x
-2 or x ![]() 0
0
Therefore the solution set = ![]() .
.
Q-5: let a, b, c be real, if ![]() has two real roots a and b where a< -1 and
has two real roots a and b where a< -1 and
b >1 then show that ![]()
Solution:
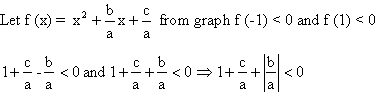
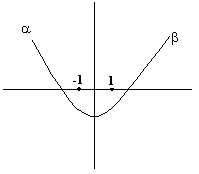
Fig (14)
Q-6: If a<b<c<d prove that the equation (x-a) (x-c) + k (x-b) (x-d) = 0 has real roots for all k ![]() R.
R.
Solution:

Equation (1) will have real roots if,
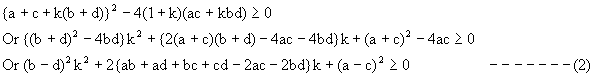
Now the discriminant of the equation corresponding (2) is,

![]()
Because a<b<c<d
Also (b-d)2>0 so (2) is true for all k ![]() R.
R.
Hence given equation have real roots.
Hard
Q-1: If p be the first of n arithmetic means between two numbers and q be the first of n harmonic means between the same two numbers, prove that q cannot lie between
![]()
Solution: Let the numbers be x, y. Let the n AMs between them be A1, A2, -------- An
Then y = (n+2) th term = x + (n+1) d (d being the common difference)
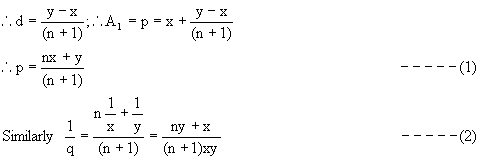
Equation (1) Þ y = (n+1) p-nx putting this in (2).