SHM -5
Question - 5. A ball is suspended by a string by length ’d' at point O. on an inclined wall angle 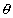 and replaced. Find the period of ascillation if (1)
and replaced. Find the period of ascillation if (1) 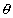 <
< 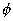 ; (2)
; (2) 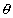 >
> 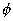 .
.
Consider l = 1 for collision.
Solution :-(1) if 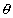 <
< 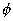 ; then ball doesn’t angular SHm with amplitude =
; then ball doesn’t angular SHm with amplitude = 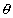 and Time period =
and Time period = 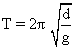 .
.
(2) if 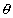 >
> 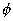 then ball collides with the ball and returns. Now if we represent this SHM on a circle :
then ball collides with the ball and returns. Now if we represent this SHM on a circle :
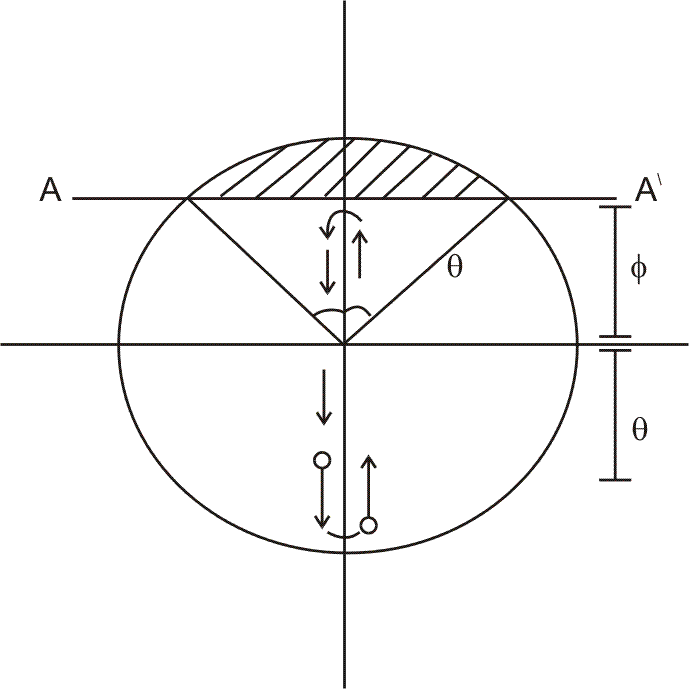
We can visualize the problem from the arrows marked At the line A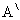 the collision occurs. which the shaded part of circle is siply cut off.
the collision occurs. which the shaded part of circle is siply cut off.
Time Period = 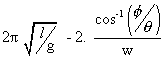
be subtracted
Also 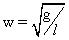
Hence 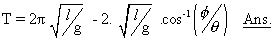
Question - 8. A simple pendulum of length ‘h’ is placed below the earth’e surface at a depth ’t'. Find time period of its ascillation ?
Solution :- At earth’s surface 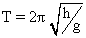 i.e.
i.e. 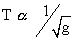
At a depth ’t' below surface :
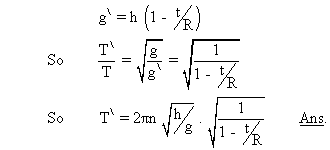
Medium
Question :- Find the mass of block which must be placed on top.
m of the block which must be placed on the top of a 6 kg cart in order that the system period is .75s. What is the minimum co-efficient of static friction 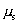 for which the block will not slip relative to the cart if the cart is displaced 50mm from the equilibrium position and realesed ? (Take
for which the block will not slip relative to the cart if the cart is displaced 50mm from the equilibrium position and realesed ? (Take 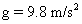 )
)
Ans :-(a)
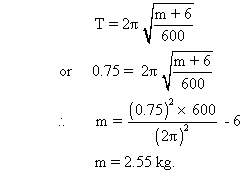
(b) Maximum accelaration of SHM is,
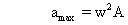
ie maximum force on mass ’m' is 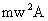 which is being provided by the force of friction between the mass and the cart.
which is being provided by the force of friction between the mass and the cart.
therefore,
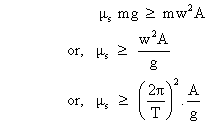
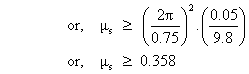
This miximumvalue of 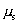 should be 0.358.
should be 0.358.
Dumb Question :- Why and when is 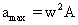 ?
?
Solution :- In SHM :
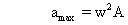
So, 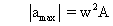
If 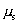 is less then this then the upper block moves (slides) over the lower one somewhere in between the mean and estreme position when the pseodo fore (wrt the lower block) becomes more than the static friction.
is less then this then the upper block moves (slides) over the lower one somewhere in between the mean and estreme position when the pseodo fore (wrt the lower block) becomes more than the static friction.
Question :-
Radius R Imagine a straight smoth tunnel mode through earth which connects any two points on its surface. Show that motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determined the time that a particle would take to go from one end to the other through the tunnel.
Ans :-
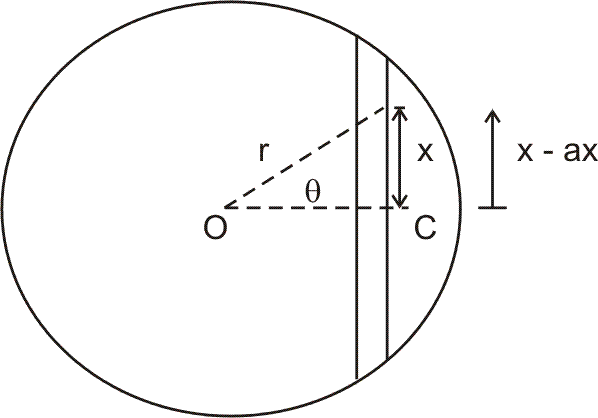
Suppose at some instant the particle is at radial distance from r centre of earth O. Since the particle is constrained to move along the tunnel, we define its position as distance x from c. Hence, equation of motion of the particle is

the gravitational force on mass at a distance r is,
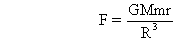 (towards 0)
(towards 0)
Therefore,
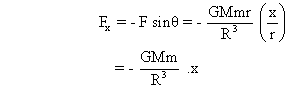
Since 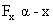 , motion is simple harmonic in nature. Further
, motion is simple harmonic in nature. Further
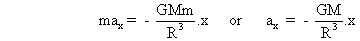
 Time period of oscillation is,
Time period of oscillation is, 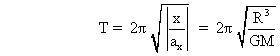
the time taken by particle to go from one end to the other is, 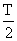
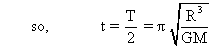
This means that as thetime period is independent of ‘r’ so wherever tunnel is dug, the body performs SHM.
Isn’t it ascinating that you drop the ball in such a tunnel and after some time it comes back to yuo!
Questions :-
sprin of force constant K and a block of mass m. It the block is slightly displaced vertically down from its equilibrium position and released, Find the period of its vertical oscillation in case (a), (b).
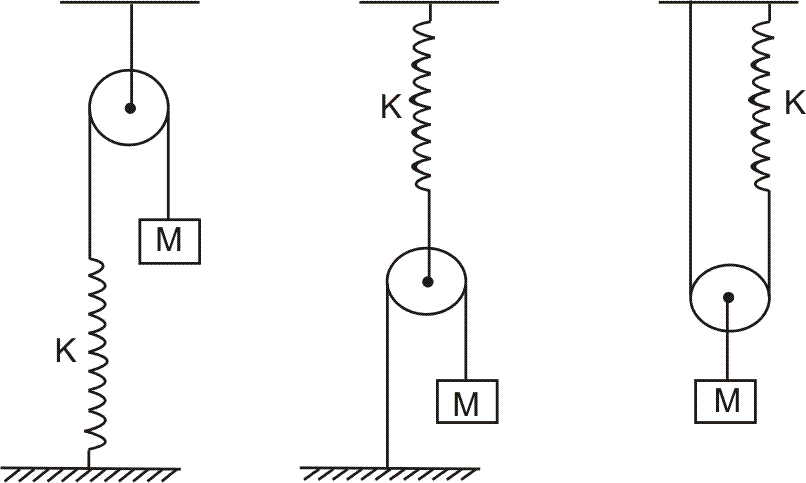
Ans :- (a)
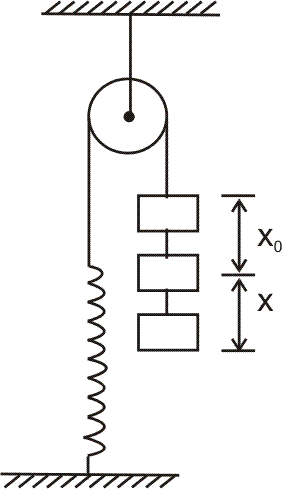
In equilibrium, 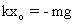 …………………. (1)
…………………. (1)
when further depressed by an amount x, net restoring fore (upwards) is,
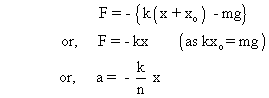
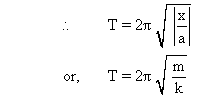
(b)
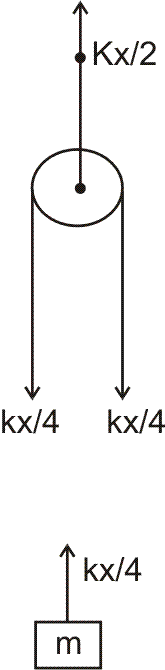
In this case, if the mass m moves down a distanc x from its equilibrium position, then pulling will move down by 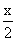 . So, the extra force in spring will be
. So, the extra force in spring will be 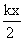 .
.