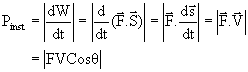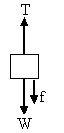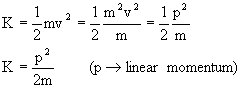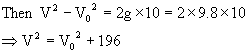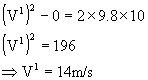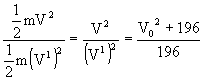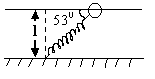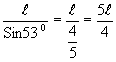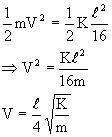|
Introduction
POWER:
Power is defined as the time rate at which work is being done or energy is being transferred.
Power can be average or instantaneous

Proof:
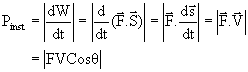
Remember power is never negative. dW stands for small work done and not difference in work because nothing called ‘difference of work’ exists.
Practical unit of power is horse power (hp)
1hp = 746W.
Illustration:
An elevator has a mass of 1000kg and carries a maximum load of 600kg. A constant frictional force of 4000N retards its upward motion, as shown in figure.
- What must be the minimum power delivered by the motor to lift the elevator at a constant speed of 3 m/sec.
- What power must the motor deliver at any instant of time, if it is designed to provide an upward acceleration of 100 m/s2
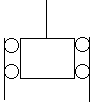
Fig (7)
Solution:
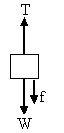
Fig (8)
Let force applied by motor be T and frictional force be f
 From f.b.d of lift From f.b.d of lift
a) T-W-f = 0 [because V is constant]
T = W+f = (1000+600)´9.8+4000
= 19680N
P = T.VCos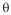
= 19680 x 3
= 5.9040 x 104 Watts
b) T-W-f = Ma
T = Ma+W+f =1600´1+1600´9.8+4000
= 21280
P = TV = 21280v Watts.
Where v is instantaneous speed of elevator at which power needs to be determined
(Without ‘v’, value of P cannot be evaluated).
ENERGY:
A body is said to possess energy if it has the capacity to do work. If some work is done by the body then it looses energy.
Energy and work are mutually interconvertible.
Various forms of Energy are:
1)Heat 2) Electrical 3) Chemical 4) Mechanical 5) Nuclear.
MECHANICAL ENERGY:
Kinetic Energy: Kinetic energy of a body is the energy possessed by a body by virtue of its motion. It is the energy associated with moving body.
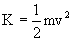 , Where, m-mass of body, v-velocity of body. , Where, m-mass of body, v-velocity of body.
Kinetic Energy is measured by the work done by moving against external impressed force, before coming to rest.
Relation between Kinetic Energy and Momentum:
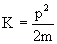
How?
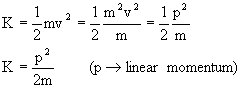
A ball falls under gravity from a height 10m, with an initial velocity V0. It hits the ground, looses 50% of its energy after collision and it rises to the same height. What is the value of V0?
Solution: Let V be the velocity when it hits the ground
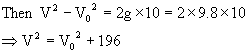
Let V1 be the velocity after impact and it reaches the same height 10m
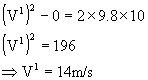
Ratio of K before and after impact = 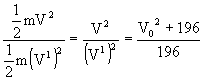
[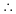 50% of K is lost] 50% of K is lost]
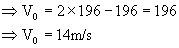
Potential Energy:
Potential Energy of a body is the energy possessed by the body by virtue of its position or configuration. Potential energy is due to the interaction between bodies.
- Physically potential energy is applicable only to the class of forces where work done against the force gets ‘stored up’ as energy. Such forces are called CONSERVATIVE FORCES.
- Conservative forces perform work whose value is path independent. Thus work done by conservative force in a closed path is zero.
- Forces which do not satisfy path independent nature are called NON-CONSERVATIVE FORCES.
- Mathematically conservative forces F(x) can be written in terms of their Potential energy forces V(x) as
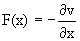
For 3-Dimensional case
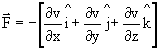
Consequently potential energy for single dimension is given by
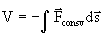
Potential Energy of Stretched spring:
F = -Kx here natural length configuration is considered as zero of potential energy.
 V-0 = V-0 =
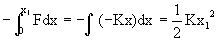
Illustration:
A spring of normal length ‘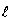 ’ and spring constant K is fixed on the ground and the other is filled with a smooth ring of mass m which slides on a horizontal rod fixed at a height also equal to l (see fig). Initially the spring makes an angle of 530 with horizontal when the system is released from rest then what is the speed of the ring? ’ and spring constant K is fixed on the ground and the other is filled with a smooth ring of mass m which slides on a horizontal rod fixed at a height also equal to l (see fig). Initially the spring makes an angle of 530 with horizontal when the system is released from rest then what is the speed of the ring?
Solution:
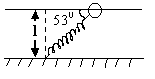
Fig (13)
In the initial position of the ring as shown in figure the length of the spring
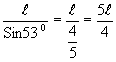
Extension 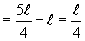
Energy stored in spring = 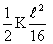
This stored energy when released becomes Kinetic energy of the ring, if V is the velocity of the ring, Kinetic energy when it is vertical = 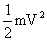
Equating two energy
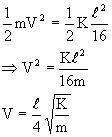
|