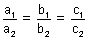3D Geometry - 1
3-D GEOMETRY
Introduction
Three dimensional geometry developed accordance to Einsteins field equations. It is useful in several branches of science like it is useful in Electromagnetism. It is used in computer alogorothms to construct 3D models that can be interactively experinced in virtual reality fashion. These models are used for single view metrology. 3-D Geometry as carrier of information about time by Einstein. 3-D Geometry is extensively used in quantum & black hole theory. Section Formula:
(1) Integral division: If R(x, y, z) is point dividing join of P(x1, y1, z1) & Q(x2, y2, z3) in ratio of m : n.
Then, x =
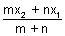 , y =
, y = 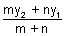 , z =
, z = 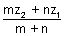
(2) External division: Coordinates of point R which divides join of P(x1, y1, z1) & Q(x2, y2, z2) externally in ratio m : n are

Illustration: Show that plane ax + by + cz + d = 0 divides line joining (x1, y1, z1) & (x2, y2, z2) in ratio of
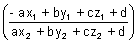
Ans: Let plane ax + by + cz + d = 0 divides line joining (x1, y1, z1) & (x2, y2, z2) in ratio K : 1
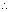 Coordinates of P
Coordinates of P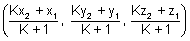
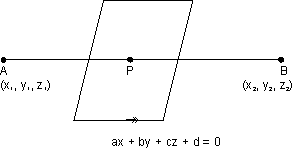
must satisfy eq. of plane.
ax + by + cz + d = 0
[Dumb Question: Why coordinates of P satisfy eq. of plane ?
Ans: Point P lies in the plane so, it satisfy eq. of plane.]
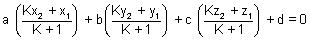
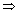 a(Kx2 + x1) + b(Ky2 + y1) + c(Kz2 + z1) + d(K + 1) = 0
a(Kx2 + x1) + b(Ky2 + y1) + c(Kz2 + z1) + d(K + 1) = 0 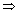 K(ax2 + by2 + cz2 + d) + (ax1 + by1 + cz1 + d) = 0
K(ax2 + by2 + cz2 + d) + (ax1 + by1 + cz1 + d) = 0 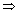 K = -
K = - 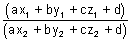
Direction Cosines:
Let
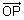 is a vector
is a vector 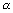 ,
,  ,
, 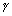 inclination with x, y & z-axis respectively. Then cos
inclination with x, y & z-axis respectively. Then cos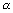 , cos
, cos & cos
& cos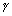 are direction cosines of
are direction cosines of 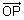 . They denoted by
. They denoted by 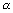 ,
,  ,
, 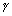
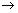 direction angles.
direction angles. & lies 0
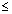
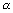 ,
,  ,
, 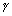
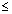
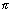
Note: (i) Direction cosines of x-axis are (1, 0, 0)
Direction cosines of y-axis are (0, 1, 0)
Direction cosines of z-axis are (0, 0, 1)
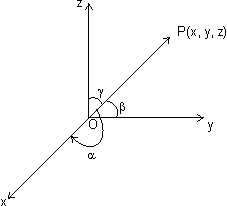
(ii) Suppose OP be any line through origin O which has direction l, m, n
(r cos
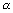 , r cos
, r cos , r cos
, r cos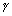 ) where OP = r
) where OP = r 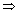 coordinates of P are (r cos
coordinates of P are (r cos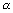 , r cos
, r cos , r cos
, r cos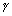 )
) or x = lr, y = mr, z = nr
(iii) l2 + m2 + n2 = 1
Proof: |
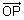 | = |
| = |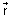 | =
| = 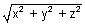
|
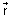 |2 = x2 + y2 + z2 = l2|
|2 = x2 + y2 + z2 = l2|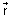 |2 + m2|
|2 + m2|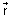 |2 + n2|
|2 + n2|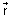 |2
|2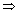 l2 + m2 + n2 = 1
l2 + m2 + n2 = 1 (iv)
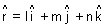
Direction ratios: Suppose l, m, & n are direction cosines of vector
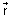 & a, b, c are no.s such that a, b, c are proportional to l, m, n. These a, b, c are c/d direction ratios.
& a, b, c are no.s such that a, b, c are proportional to l, m, n. These a, b, c are c/d direction ratios.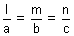 = k
= kSuppose a, b, c are direction ratios of vector
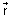 having direction cosines l, m, n. Then,
having direction cosines l, m, n. Then, 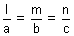 =
= 
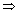 l =
l =  a, m =
a, m =  b, n =
b, n =  c
c 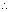 l2 + m2 + n2 = 1
l2 + m2 + n2 = 1 a2
 2 + b2
2 + b2 2 + c2
2 + c2 2 = 1
2 = 1 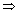
 = ±
= ± 
l = ±
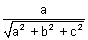 , m = ±
, m = ± 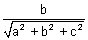 , n = ±
, n = ± 
Note: (i) If
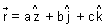 having direction cosines l, m, n. Then, l =
having direction cosines l, m, n. Then, l = 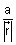 , m =
, m = 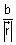 , n =
, n = 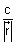
(ii) Direction ratios of line joining two given points
(x1, y1, z1) & (x2, y2, z2) is (x2 - x1, y2 - y1, z2 - z1)
(iii) If direction ratio’s of
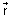 are a, b, c
are a, b, c 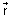 =
= 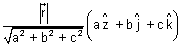
(iv) Projection of segment joining points P(x1, y1, z1) and Q(x2, y2, z2) on a line with direction cosines l, m, n, is:
(x2 - x1)l + (y2 - y1)m + (z2 - z1)n
Illustration: If a line makes angles
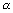 ,
,  &
& 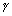 with coordinate axes, prove that sin2
with coordinate axes, prove that sin2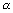 + sin2
+ sin2 + sin2
+ sin2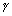 = 2
= 2 Ans: Line is making
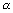 ,
,  &
& 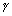 with coordinate axes.
with coordinate axes.Then, direction cosines are l = cos
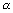 , m = cos
, m = cos & n = cos
& n = cos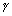 .
.But l2 + m2 + n2 = 1
cos2
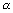 + cos2
+ cos2 + cos2
+ cos2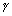 = 1
= 1 1 - sin2
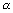 + 1 - sin2
+ 1 - sin2 + 1 - cos2
+ 1 - cos2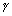 = 1
= 1 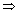 sin2
sin2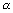 + sin2
+ sin2 + sin2
+ sin2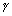 = 2
= 2 Angle b/w two vectors in terms of direction cosines & direction ratios:
(i) Suppose
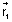 &
& 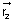 are two vectors having d.c’s l1, m1, n1 & l2, m2, n2 respectively. Then,
are two vectors having d.c’s l1, m1, n1 & l2, m2, n2 respectively. Then, 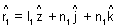 &
& 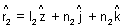
Dumb Question: How
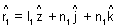 ?
? Ans:

But l12 + m12 + n12 = 1
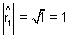
So,
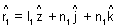
cos
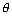 =
= 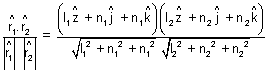
cos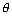 = l1l2 + m1m2 + n1n2 = l1l2 + m1m2 + n1n2 |
(ii) IF a1, b1, c1 and a2, b2, c2 are d.r.s of
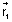 &
& 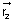 . Then
. Then 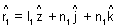 &
& 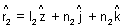
cos
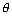 =
= 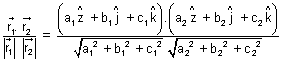
cos
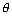 =
= 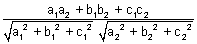
Note: (i) If two lines are
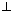 then,
then, cos
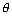 = 0 or l1l2 + m1m2 + c1c2 = 0
= 0 or l1l2 + m1m2 + c1c2 = 0 or a1a2 + b1b2 + c1c2 = 0
(ii) If two lines are || then
cos
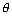 = 1 or
= 1 or 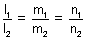
or