3D Geometry - 3
Introduction
Vector Form:
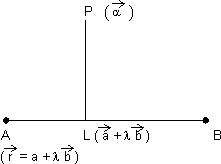
Since L lies on line AB
P.V. of L = P.V. of line AB
=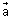 +
+ 
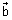
dr's of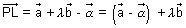
Since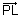
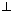
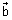
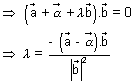
 P.V. of L is
P.V. of L is 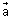 +
+ 
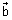
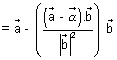
Reflection of point in straight line:
Castesian Form:
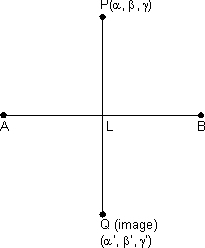
From above, we get coordinate of L(foot of )
)
But L is mid point of PQ
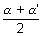 = x1+ a
= x1+ a ,
, 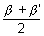 = y1 + b
= y1 + b ,
, 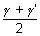 = z1 + c
= z1 + c

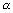 ' = 2(x1 + a
' = 2(x1 + a ) -
) - 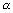 ,
, 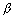 ' = 2(y1 + b
' = 2(y1 + b ) -
) - 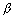 ,
, 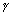 ' = 2(z1 + c
' = 2(z1 + c ) -
) - 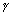
Vector Form:

From above, we get
P.V. of L,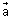 +
+ 
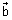
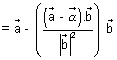
Let P.V. of Q is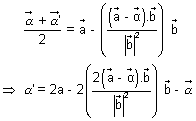
Since L is mid point of PQ
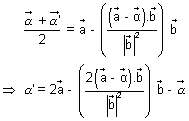
Illustration: Find reflection of point P(2, 3, 1) in line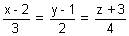
Ans:
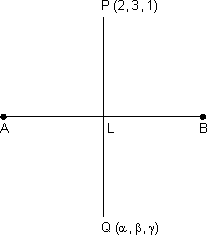
Since L lies on line AB
 coordinate of L (3
coordinate of L (3 + 2, 2
+ 2, 2 + 1, 4
+ 1, 4 - 3)
- 3)
DR's of PL are
= (3 + 2 - 2, 2
+ 2 - 2, 2 + 1 - 3, 4
+ 1 - 3, 4 - 3 - 1)
- 3 - 1)
= (3 , 2
, 2 - 2, 4
- 2, 4 - 4)
- 4)
DR's of AB are (3, 2, 4)
Since PL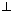 AB
AB
3(3 ) + 2(2
) + 2(2 - 2) + 4(4
- 2) + 4(4 - 4) = 0
- 4) = 0
9 + 4
+ 4 - 4 + 16
- 4 + 16 - 16 = 0
- 16 = 0
29 = 20
= 20  =
= 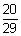
Since L is mid point of PQ
So,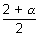 = 3
= 3 + 2,
+ 2, 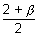 = 2
= 2 + 1,
+ 1, 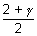 = 4
= 4 - 3
- 3
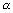 = (6
= (6 + 4 - 2),
+ 4 - 2), 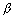 = (4
= (4 + 2 - 3),
+ 2 - 3), 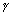 = 8
= 8 - 6 - 1
- 6 - 1
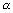 = 6
= 6 + 2,
+ 2, 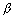 = 4
= 4 - 1,
- 1, 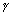 = 8
= 8 - 7
- 7
where =
= 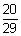
Skew lines: Those lines which do not lies in same plane.
Shortest distence b/w two skew lines:
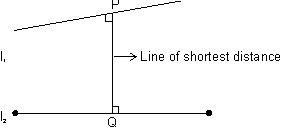
The line which is to both line l1 & l2 are c/d line of shortest distance.
to both line l1 & l2 are c/d line of shortest distance.
Vector Form:
Let l1 & l2 are:
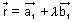 &
& 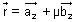 respectively.
respectively.
Since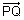 is
is 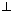 to both l1 & l2 which are parallel to
to both l1 & l2 which are parallel to 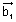 &
& 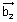
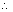
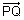 is || to
is || to 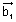 x
x 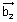
Let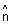 be unit vector along
be unit vector along 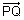 , then
, then 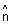 = ±
= ± 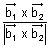
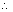 PQ = Projection of
PQ = Projection of 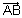 on
on 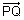

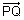 =
= 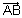 .
.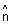
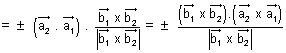
Dumb Question: How PQ = Projection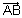 on
on 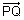 ?
?
Ans: Form fig., it is clear that PQ is projection of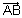 on
on 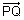 .
.
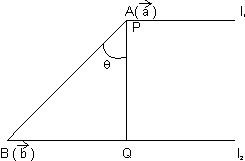
PQ =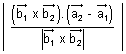
Cartesian form: Two skew lines
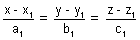 &
& 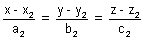
Shortest distance :
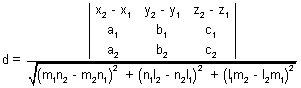
Condition for lines to intersect:
Two lines intersects if shortest distance = 0
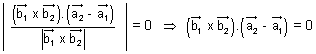
or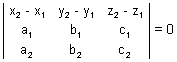
Shortest distance b/w parallel line:
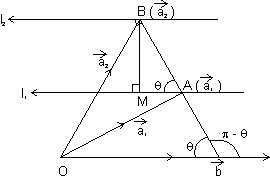
Let l1 & l2 are
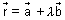
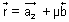 respectively
respectively
& BM is shortest distance b/w l1 & l2
sin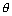 =
= 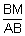
 BM = AB sin
BM = AB sin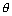 = |
= |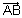 | sin
| sin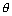
|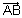 x
x 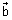 | = |
| = |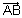 | |
| |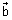 | sin(
| sin(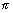 -
- 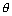 )
)
= |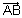 | |
| |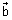 | sin
| sin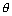 = (|
= (|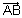 | sin
| sin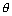 ) |
) |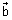 | =
| =
Dumb Question: Why we have taken sin(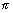 -
- 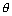 ) ?
) ?
Ans:
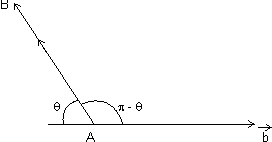
Since direction of vector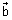 is opposite to || lines. So, we have taken (
is opposite to || lines. So, we have taken (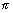 -
- 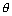 ) instead of
) instead of 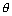
 BM =
BM = 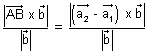
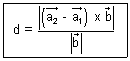
Illustration: Find shortest distance b/w lines:
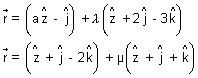
Ans: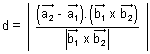
On comparing
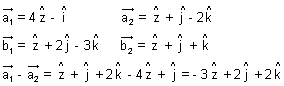
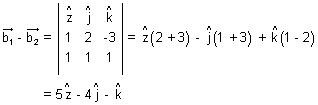
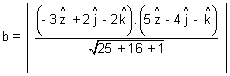
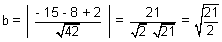
Plane:
(i) Eq. of plane passing through a given point (x1, y1, z1) is:
a(x - x1) + b(y - y1) + c(z - z1) = 0 where a, b, c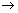 constants.
constants.
Proof: General eq. of plane is ax + by + cz + d = 0 ....................................... (i)
It is passes through (x1, y1, z1)
 ax1 + by1 + cz1 + d = 0 ............................................. (ii)
ax1 + by1 + cz1 + d = 0 ............................................. (ii)
By (i) - (ii), we get
a(x - x1) + b(y - y1) + c(z - z1) = 0
Intercept form of a plane:
eq. of plane of intercepting lengths a, b & c with x, y & z-axis respectively is,
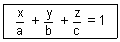
Illustration: A variable plane moves in such a way that sum of reciprocals of its intercepts on 3 coordinate axes is constant. Show that plane passes through fixed point.
Ans: Let eq. of plane is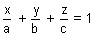 . Then, intercepts of plane with axes are:
. Then, intercepts of plane with axes are:
A(a, 0, 0), B(0, b, 0), c(0, 0, c)
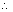
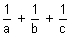 = constant (k) (given)
= constant (k) (given)

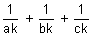 = 1 & comparing with fixed point
= 1 & comparing with fixed point 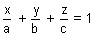
x =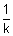 , y =
, y = 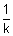 , z =
, z = 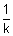
This shows plane passes through fixed point (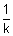 ,
, 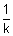 ,
, 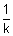 )
)
Vector eq. of plane passing through a given point & normal to given vector:
VEctor eq. of plane passing through u point of P.V.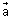 & normal to vector
& normal to vector 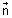 is (
is ( -
- 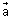 ).
).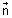 = 0
= 0
Dumb Question: What is normal to vector ?
Ans: Plane normal to vector means the every line in plane is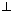 to that given vector.
to that given vector.
Proof: Let plane passes through A(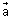 ) & normal to vector
) & normal to vector 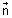 &
&  be P.V. of every point 'P' on palne.
be P.V. of every point 'P' on palne.
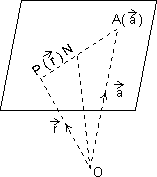
Since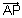 lies in plane &
lies in plane & 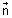 is normal to plane.
is normal to plane.
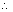
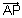
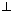
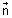

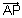 .
.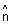 = 0
= 0
 (
( -
- 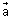 ).
).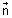 = 0 (
= 0 (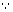
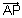 =
=  -
- 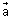 )
)
eq. of plane ( -
- 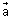 ).
).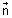 = 0
= 0
Eq. of plane in normal form:
Vector eq. of plane normal to unit vector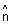 & at O distance d from origin is
& at O distance d from origin is  .
.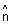 = d.
= d.
Proof:
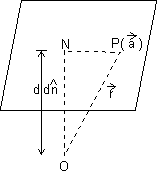
ON is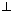 to plane such that
to plane such that 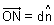 &
& 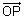 =
= 
Since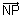
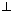 .
.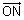 = 0
= 0
 (
(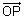 -
- 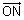 ).
).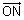 = 0
= 0
 (
( - d
- d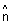 ).d
).d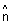 = 0
= 0 
 .d
.d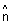 - d2
- d2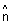 .
.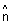 = 0
= 0
 d(
d( .
.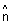 ) - d2 = 0
) - d2 = 0 
 .
. = d
= d
eq. of plane is .
. = d
= d
Cartesian Form: Let l, m, n be d.r.'s of normal to given plane & P is length of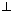 from origin to plane, then eq. of plane is lx + my + nz = P.
from origin to plane, then eq. of plane is lx + my + nz = P.
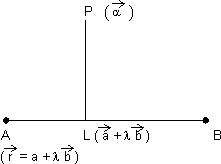
Since L lies on line AB
P.V. of L = P.V. of line AB
=
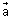 +
+ 
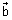
dr's of
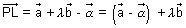
Since
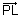
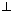
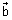
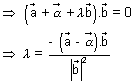
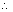 P.V. of L is
P.V. of L is 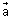 +
+ 
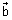
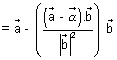
Reflection of point in straight line:
Castesian Form:

From above, we get coordinate of L(foot of
 )
)But L is mid point of PQ
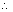
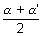 = x1+ a
= x1+ a ,
, 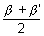 = y1 + b
= y1 + b ,
, 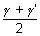 = z1 + c
= z1 + c

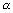 ' = 2(x1 + a
' = 2(x1 + a ) -
) - 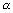 ,
, 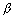 ' = 2(y1 + b
' = 2(y1 + b ) -
) - 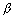 ,
, 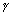 ' = 2(z1 + c
' = 2(z1 + c ) -
) - 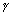
Vector Form:

From above, we get
P.V. of L,
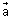 +
+ 
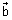
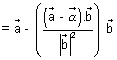
Let P.V. of Q is
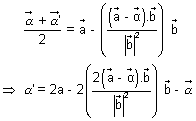
Since L is mid point of PQ
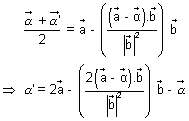
Illustration: Find reflection of point P(2, 3, 1) in line
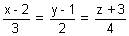
Ans:

Since L lies on line AB
 coordinate of L (3
coordinate of L (3 + 2, 2
+ 2, 2 + 1, 4
+ 1, 4 - 3)
- 3)DR's of PL are
= (3
 + 2 - 2, 2
+ 2 - 2, 2 + 1 - 3, 4
+ 1 - 3, 4 - 3 - 1)
- 3 - 1)= (3
 , 2
, 2 - 2, 4
- 2, 4 - 4)
- 4)DR's of AB are (3, 2, 4)
Since PL
 AB
AB3(3
 ) + 2(2
) + 2(2 - 2) + 4(4
- 2) + 4(4 - 4) = 0
- 4) = 09
 + 4
+ 4 - 4 + 16
- 4 + 16 - 16 = 0
- 16 = 029
 = 20
= 20  =
= 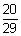
Since L is mid point of PQ
So,
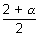 = 3
= 3 + 2,
+ 2, 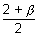 = 2
= 2 + 1,
+ 1, 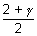 = 4
= 4 - 3
- 3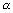 = (6
= (6 + 4 - 2),
+ 4 - 2), 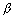 = (4
= (4 + 2 - 3),
+ 2 - 3), 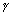 = 8
= 8 - 6 - 1
- 6 - 1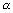 = 6
= 6 + 2,
+ 2, 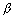 = 4
= 4 - 1,
- 1, 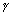 = 8
= 8 - 7
- 7where
 =
= 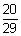
Skew lines: Those lines which do not lies in same plane.
Shortest distence b/w two skew lines:

The line which is
 to both line l1 & l2 are c/d line of shortest distance.
to both line l1 & l2 are c/d line of shortest distance.Vector Form:
Let l1 & l2 are:
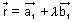 &
& 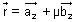 respectively.
respectively.Since
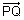 is
is 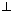 to both l1 & l2 which are parallel to
to both l1 & l2 which are parallel to 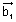 &
& 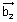
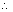
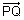 is || to
is || to 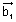 x
x 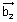
Let
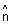 be unit vector along
be unit vector along 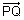 , then
, then 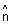 = ±
= ± 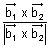
 PQ = Projection of
PQ = Projection of 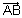 on
on 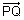

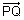 =
= 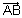 .
.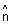
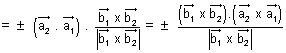
Dumb Question: How PQ = Projection
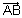 on
on 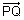 ?
?Ans: Form fig., it is clear that PQ is projection of
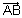 on
on 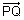 .
.
PQ =
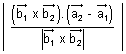
Cartesian form: Two skew lines
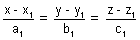 &
& 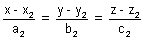
Shortest distance :
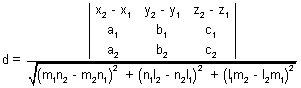
Condition for lines to intersect:
Two lines intersects if shortest distance = 0
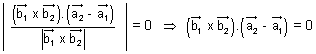
or
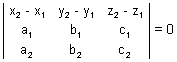
Shortest distance b/w parallel line:

Let l1 & l2 are
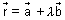
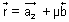 respectively
respectively& BM is shortest distance b/w l1 & l2
sin
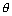 =
= 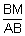
 BM = AB sin
BM = AB sin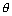 = |
= |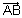 | sin
| sin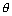
|
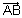 x
x 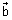 | = |
| = |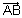 | |
| |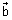 | sin(
| sin(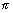 -
- 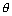 )
)= |
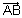 | |
| |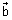 | sin
| sin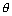 = (|
= (|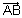 | sin
| sin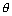 ) |
) |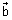 | =
| =Dumb Question: Why we have taken sin(
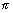 -
- 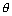 ) ?
) ?Ans:

Since direction of vector
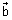 is opposite to || lines. So, we have taken (
is opposite to || lines. So, we have taken (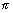 -
- 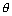 ) instead of
) instead of 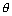
 BM =
BM = 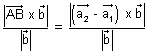
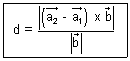
Illustration: Find shortest distance b/w lines:
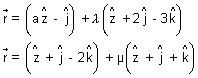
Ans:
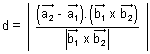
On comparing
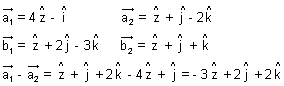
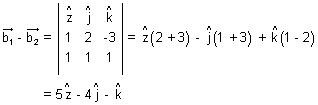
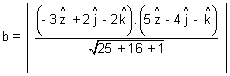
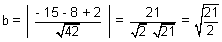
Plane:
(i) Eq. of plane passing through a given point (x1, y1, z1) is:
a(x - x1) + b(y - y1) + c(z - z1) = 0 where a, b, c
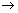 constants.
constants.Proof: General eq. of plane is ax + by + cz + d = 0 ....................................... (i)
It is passes through (x1, y1, z1)
 ax1 + by1 + cz1 + d = 0 ............................................. (ii)
ax1 + by1 + cz1 + d = 0 ............................................. (ii)By (i) - (ii), we get
a(x - x1) + b(y - y1) + c(z - z1) = 0
Intercept form of a plane:
eq. of plane of intercepting lengths a, b & c with x, y & z-axis respectively is,
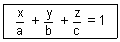
Illustration: A variable plane moves in such a way that sum of reciprocals of its intercepts on 3 coordinate axes is constant. Show that plane passes through fixed point.
Ans: Let eq. of plane is
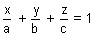 . Then, intercepts of plane with axes are:
. Then, intercepts of plane with axes are:A(a, 0, 0), B(0, b, 0), c(0, 0, c)
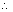
 = constant (k) (given)
= constant (k) (given)
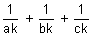 = 1 & comparing with fixed point
= 1 & comparing with fixed point 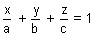
x =
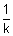 , y =
, y = 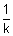 , z =
, z = 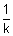
This shows plane passes through fixed point (
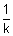 ,
, 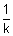 ,
, 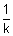 )
)Vector eq. of plane passing through a given point & normal to given vector:
VEctor eq. of plane passing through u point of P.V.
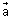 & normal to vector
& normal to vector 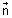 is (
is ( -
- 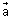 ).
).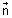 = 0
= 0Dumb Question: What is normal to vector ?
Ans: Plane normal to vector means the every line in plane is
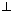 to that given vector.
to that given vector.Proof: Let plane passes through A(
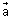 ) & normal to vector
) & normal to vector 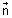 &
&  be P.V. of every point 'P' on palne.
be P.V. of every point 'P' on palne.
Since
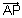 lies in plane &
lies in plane & 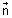 is normal to plane.
is normal to plane.
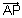
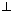
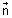

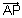 .
.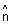 = 0
= 0 (
( -
- 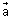 ).
).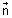 = 0 (
= 0 (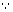
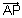 =
=  -
- 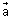 )
)eq. of plane (
 -
- 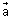 ).
).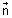 = 0
= 0Eq. of plane in normal form:
Vector eq. of plane normal to unit vector
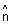 & at O distance d from origin is
& at O distance d from origin is  .
.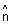 = d.
= d.Proof:

ON is
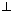 to plane such that
to plane such that 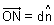 &
& 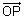 =
= 
Since
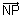
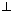 .
.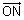 = 0
= 0 (
(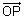 -
- 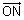 ).
).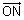 = 0
= 0 (
( - d
- d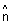 ).d
).d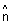 = 0
= 0 
 .d
.d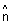 - d2
- d2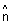 .
.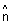 = 0
= 0 d(
d( .
.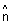 ) - d2 = 0
) - d2 = 0 
 .
.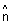 = d
= deq. of plane is
 .
.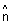 = d
= dCartesian Form: Let l, m, n be d.r.'s of normal to given plane & P is length of
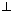 from origin to plane, then eq. of plane is lx + my + nz = P.
from origin to plane, then eq. of plane is lx + my + nz = P.