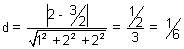3D Geometry - 4
Introduction
Dumb Question: How this lx + my + nz = P is eq. of plane ? Ans: Since
 .
.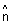 = P = d is eq. of plane
= P = d is eq. of plane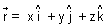 &
& 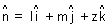
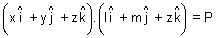
 lx + my + nz = P
lx + my + nz = PIllustration: Find vector eq. of plane which is at a distance of 8 units from origin & which is normal to vector
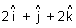 .
. Ans: d = 8 &
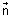 =
= 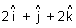
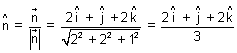
eq. of plane is,
 .
.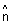 = d
= d 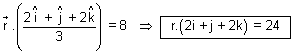
Eq. of plane passing through 3 given points:
Eq. of plane passing through three points A, B, C having P.V.’s
 ,
,  ,
,  respectivelt.
respectivelt. Let
 be P>V> of any point P is the plane.
be P>V> of any point P is the plane. So, vectors,
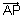 =
=  -
-  ,
,  =
=  -
-  ,
, 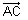 =
=  -
-  are coplanar
are coplanar Hence,
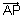 .(
.( x
x 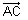 ) = 0
) = 0 (
 -
-  ).{(
).{( -
-  ) x (
) x ( -
-  )} = 0
)} = 0 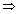 (
( -
-  ).(
).( x
x  -
-  x
x  -
-  x
x  -
-  x
x  ) = 0
) = 0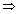 (
( -
-  ).(
).( x
x  +
+  x
x  +
+  x
x  ) = 0
) = 0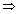
 .(
.( x
x  +
+  x
x  +
+  x
x  ) =
) =  .(
.( x
x  ) +
) +  .(
.( x
x  ) +
) +  .(
.( x
x  )
) 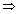 [
[

 ] + [
] + [

 ] + [
] + [

 ] = [
] = [

 ]
]Note: If P is length of
 from origin on this plane,
from origin on this plane,then P =
 n = |
n = | x
x  +
+  x
x  +
+  x
x  |
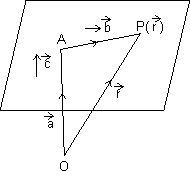
| Eq. of plane that passes through a point A with position vector
 & is || to given vectors
& is || to given vectors  &
&  :
: Derivation:
Let
 be P.V. of any point P in plane
be P.V. of any point P in plane Then,
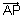 =
= 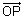 -
- 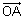 =
=  -
- 
Sincen
 x
x  are || to plane.
are || to plane.So, vector
 -
-  ,
,  &
&  are coplanar
are coplanar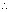 (
( -
-  ).(
).( x
x  ) = 0
) = 0 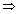
 .(
.( x
x  ) =
) =  .(
.( x
x  )
) 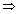 [
[

 ] = [
] = [

 ]
] Cartesian form: Eq. of plane passing through a point (x1, y1, z1) & || to two lines having direction ratios (
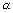 1,
1, 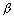 1,
1,  1) & (
1) & (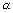 2,
2, 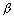 2,
2,  2) is:
2) is: 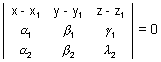
Illustration: Find eq. of plane passing through points
P(1, 1, 1), Q(3, -1, 2), R(-3, 5, -4).
Ans: Let eq. of plane is ax + by + cz + d = 0
It passes through P(1, 1, 1). So,
eq. of plane
a(x - 1) + b(y - 1) + c(z - 1) = 0 …………………………………… (i)
But it also passes through Q & R
2a - 2b + c = 0] x (- 2)
- 4a + 4b - 5c = 0
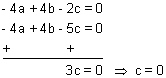
Similarly a = 6, b = 6
Putting these in eq. (i)
We get, 6(x - 1) + 6(y - 1) = 0
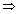 x + y = 2
x + y = 2 Angle b/w two planes:
 .
. = d1
= d1  .
.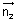 = d2 are two planers, then
= d2 are two planers, then cos
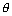 =
= 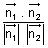
Note: Angle b/w planes is defined as angle b/w their normals.
Cartesion Form: Let planes are a1x + b1y + c1z + d1 = 0 & a2x + b2y + c2z + d2 = 0
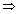 cos
cos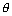 =
= 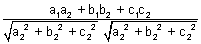
Condition for
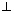 :
: 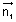 .
.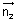 = 0
= 0 or a1a2 + b1b2 + c1c2 = 0
Condition for parallelism:
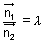 or
or 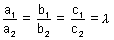
Angle b/w line & a plane:
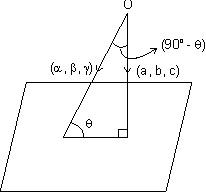
If
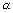 ,
, 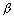 ,
,  be direction ratios of line & ax + by + cz + d = 0 be eq. of plane in which normal has d.r’s a, b, c. Q is angle b/w line & plane.
be direction ratios of line & ax + by + cz + d = 0 be eq. of plane in which normal has d.r’s a, b, c. Q is angle b/w line & plane.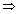 cos(900 -
cos(900 - 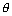 ) =
) = 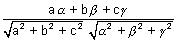
Vector form: If
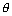 is angle b/w line
is angle b/w line 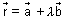 & plane
& plane  .
.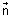 = d
= d 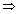 sin
sin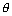 =
= 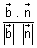
Illustration: Find angle b/w line
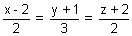 & 3x + 2y - 2z + 3 = 0.
& 3x + 2y - 2z + 3 = 0. Ans: D.r’s of line are 2, 3, 2 & d.r’s of normal to plane are 3, 2, - 2
sin
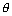 =
= 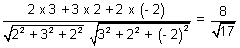
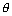 = sin-1
= sin-1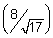
Eq. of plane passing through the Line of Intersection of planes
a1x + b1y + c1z + d1 = 0 & a2x + b2y + c2z + d2 = 0 is
(a1x + b1y + c1z + d1) + k(a2x + b2y + c2z + d2) = 0
Dumb Question: How this eq. is that of required plane ?
Ans: Let P(
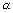 ,
, 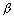 ,
,  ) be point on line of intersection of two planes. So, it lies on both the planes.
) be point on line of intersection of two planes. So, it lies on both the planes. i.e. a1
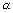 + b1
+ b1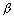 + c1
+ c1 + d1 = 0
+ d1 = 0 & a2
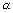 + b2
+ b2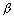 + c2
+ c2 + d2 = 0
+ d2 = 0 So, point P(
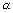 ,
, 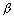 ,
,  ) should lie on required plane.
) should lie on required plane. i.e. (a1
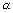 + b1
+ b1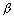 + c1
+ c1 + d1) + k(a2
+ d1) + k(a2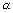 + b2
+ b2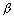 + c2
+ c2 + d2 ) = 0
+ d2 ) = 0  P(
P(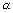 ,
, 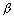 ,
,  ) lies on. plane (a1x + b1y + c1z + d1) + k(a2x + b2y + c2z + d2) = 0
) lies on. plane (a1x + b1y + c1z + d1) + k(a2x + b2y + c2z + d2) = 0 Vector Form:
 .
.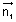 = d1 &
= d1 &  .
.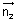 = d2
= d2So, eq. of required plane is (
 .
.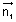 - d1) + k(
- d1) + k( .
.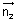 - d2) = 0
- d2) = 0 Illustration: Find eq. of plane constaining line of intersection of plane x - y + z + 7 = 0 and x + 3y + 2z + 5 = 0 & passing through (1, 2, 2).
Ans: Eq. of plane through line of intersection of given planes is,
(x - y + z + 7) +
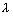 (x + 3y + 2z + 5) = 0 ………………………………… (i)
(x + 3y + 2z + 5) = 0 ………………………………… (i) It passes through (1, 2, 3)
(1 - 2 + 2 + 7) +
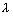 (1 + 3 x 2 + 2 x 2 + 5) = 0
(1 + 3 x 2 + 2 x 2 + 5) = 0 8 +
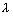 (7 + 4 + 5)
(7 + 4 + 5) 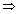
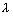 =
= 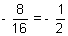
Putting
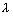 = -
= - 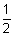 in eq. (i)
in eq. (i) We get,
(x - y + z + 7) + (-
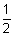 )(x + 3y + 2z + 5) = 0
)(x + 3y + 2z + 5) = 0 2x - 2y + 2z + 14 - x - 3y - 2z - 5 = 0
x - 5y + 9 = 0
Two sides of plane:
If ax + by + cz + d = 0 be a plane then points (x1, y1, z1) & (x2, y2, z2) are points lies on
Same side if
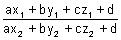 > 0 & opposite side if
> 0 & opposite side if 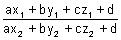 < 0
< 0 Distance of point from a plne:
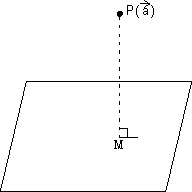
Length of
 from a point having P.V.
from a point having P.V.  to plane
to plane  .
.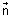 = d is given by
= d is given by P =
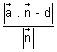
Proof: PM is length of
 from P to plane. Since line PM passes through P(
from P to plane. Since line PM passes through P( ) & || to vector
) & || to vector  which is normal to plane.
which is normal to plane. 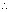 eq. of line
eq. of line  =
=  x
x 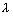
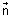 ………………………………………………. (i)
………………………………………………. (i) Since point M is intersection of line & plane. So, it lies on line as well as plane
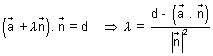
Putting
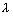 in eq. (i)
in eq. (i)  =
=  +
+ 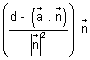
 = P.V. of M - P.V. of P =
= P.V. of M - P.V. of P =  +
+ 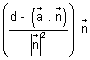 -
- 
Dumb Question: How P.V. of M is
 +
+ 
Ans: M lies on line as well as plane. On solving value of
 for line eq. We get P.V. of M.
for line eq. We get P.V. of M. So, this is P.V. of M
PM = |
 | =
| = 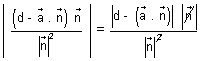
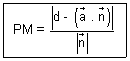
Cartesian Form: Length of
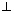 from point P(x1, y1, z1) to plane ax + by + cz + d = 0, Then eq. of PM is
from point P(x1, y1, z1) to plane ax + by + cz + d = 0, Then eq. of PM is  = r
= r [Dumb Question: How this eq. of PM comes ?
Ans: It is passes through point (x1, y1, z1) & || to normal of plane so, we get this eq.]
Coordinates of any point on PM are
(x1 + ar, y1 + br, z1 + cr)
But this also coordinate of M & M also lies on plane
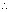 a(x1 + ar) + b(y1 + br) + c(z1 + cr) + d = 0
a(x1 + ar) + b(y1 + br) + c(z1 + cr) + d = 0 i.e. r = -
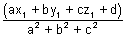
PM =
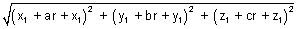
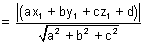
Distance b/w parallel planes:
Distance b/w || planes is difference of length of
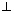 from origin to two planes.
from origin to two planes. Let ax + by + cz + d1 = 0 & ax + by + cz + d2 = 0
D =
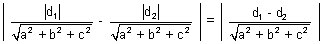
Vector Form:
 .
.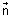 = d1 &
= d1 &  .
.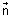 = 2
= 2 
Illustion: Find distance b/w parallel planes
x + 2y + 2z + 2 = 0 & 2x + 4y + 4z + 3 = 0
Ans: Distance b/w ax + by + cz + d1 = 0 & ax + by + cz + d2 = 0 is
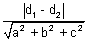
x + 2y + 2z + 2 = 0 & x + 2y + 2z +
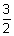 = 0
= 0