3D Geometry - 5
Equation of planes Bisecting Angle b/w Two planes:
Eq. of planes bisceting angle b/w planes, a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is,
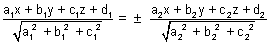
Proof: Let P(x, y, z) be point on plane bisecting angle b/w two planes 7 PL & PM is length of  from P to planes.
from P to planes.
By property of angle bisector.
PL = PM
[Dumb Question: How PL = PM ?
Ans: In fig 1.
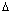 OPL & OPM are congruent by AAA symmetry. So, all sides are equal.
OPL & OPM are congruent by AAA symmetry. So, all sides are equal. So, PL = PM.]
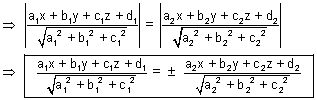
Note: (i) Eq. of bisector of angle b/w two planes containing origin is
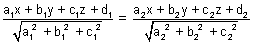
(ii) Bisector of acute & obtuse angles b/w:
Let a1x + b1y + c1z + d1 = 0
& a2x + b2y + c2z + d2 = 0 where d1, d2 > 0
(a) If a1a2 + b1b2 + c1c2 > 0, origin lies in obtuse angle bisector & eq. of bisector of acute angle is
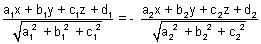
(b) If a1a2 + b1b2 + c1c2 < 0, origin lies in atute angle bisector & eq. of acute angle bisector is
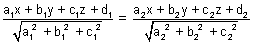
Illustration: Find eq. of bisector planes of angle b/w planes 2x + y - 2z + 3 = 0 & 3x + 2y - 6z + 8 = 0 specify obtuse & acute angle bisectors.
Ans: 2x + y - 2z + 3 = 0 & 3x + 2y - 6z + 8 = 0 where d1, d2 > 0
Now a1a2 + b1b2 + c1c2 = 2 x 3 + 1 x 2 + 2 x 6 > 0
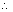
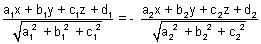 ...................................... (i)
...................................... (i) (i) is obtuse angle bisector plane
&
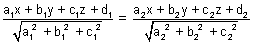 ................................................ (ii)
................................................ (ii)(ii) is acute angle bisector plane.
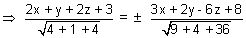
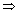 14x + 7y - 14z + 21 = ± 9x + 6y - 18z + 24
14x + 7y - 14z + 21 = ± 9x + 6y - 18z + 24 For obtuse angle bisector plane, Take -ve sign
5x + y + 4z - 3 = 0
Intersection of line & plane:
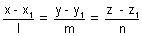 = r & plane ax + by + cz + d = 0
= r & plane ax + by + cz + d = 0 
Let P be point of intersection coordinate of P(x1 + lr, y1 + mr, z1 + nr)
But it satisfy eq. of plane.
a(x1 + lr) + b(y1 + mr) + c(z1 + nr)
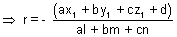
Condition for line to be || to a plane:
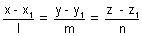 be || to plane ax + by + cz + d = 0
be || to plane ax + by + cz + d = 0 if al + bm + cm = 0 or sin
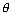 = 0
= 0Condition for a line to lie in the plane:
line
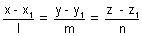 lie in plane ax + by + cz + d = 0
lie in plane ax + by + cz + d = 0 if al + bm + cn = 0 & ax1 + by1 + cz1 + d = 0
Dumb Question: How line be || to plane if al + bm + cn = 0 ?
Ans: If
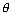 is angle b/w line & plane, then
is angle b/w line & plane, then sin
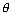 =
= 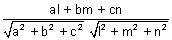 [Previously desired]
[Previously desired] line is || to plane if sin
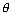 = 0 or al + bm + cn = 0
= 0 or al + bm + cn = 0 Sphere:
Equation of sphere whose centre is
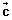 & radius is a:
& radius is a: 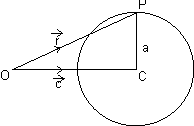
In
 OPC,
OPC, 
 |
|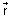 -
- 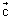 | = CP = a (radius)
| = CP = a (radius) 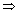 |
|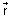 -
- 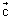 |2 = a2
|2 = a2 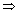 (
(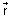 -
- 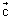 ).(
).(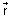 -
- 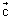 ) = A2
) = A2 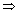 R2 - 2
R2 - 2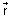 .
.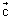 + c2 = a2
+ c2 = a2 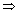 r2 - 2
r2 - 2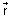 .
.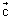 + (c2 - a2) = 0
+ (c2 - a2) = 0 Cartesian Form:
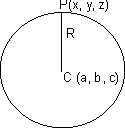
From Fig. CP = R
CP2 = R2
By distance formula.
(x - a)2 + (y - b)2 + (z - c)2 = R2
GEneral eq. of sphere:
x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0 is a sphere with centre (- u, - v, - w) &
radius =
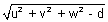
Illustration: Find centre & radius of sphere 2x2 + 2y2 + 2z2 - 2x - 4y + 2z + 3 = 0
Ans: 2x2 + 2y2 + 2z2 - 2x - 4y + 2z + 3 = 0
or x2 + y2 + z2 - x - 2y + z +
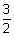 = 0
= 0 centre is (-
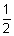 coeff. of x, -
coeff. of x, - 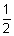 coeff. of y, -
coeff. of y, - 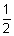 coeff. of z)
coeff. of z)  centre (
centre (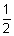 , 1, -
, 1, - 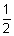 )
) radius =
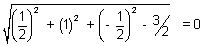
Thus sphere is point circle.
Diameter form of Eq. of sphere:
Vector Form: Suppose
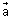 &
& 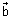 be P.V of extremities A & B of diameter AB of sphere. Let
be P.V of extremities A & B of diameter AB of sphere. Let 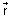 be P.V. of any point P on sphere. Then,
be P.V. of any point P on sphere. Then, 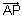 =
= 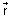 -
- 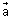 & B
& B  =
= 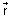 -
- 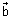
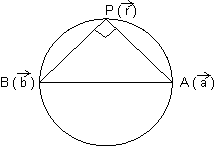
Since, diameter of sphere subtends a right
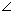 at any point of sphere.
at any point of sphere. 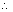
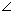 APB =
APB = 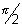
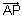 .
. = 0
= 0 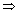 (
(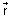 -
- 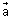 ).(
).(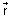 -
- 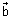 ) = 0
) = 0 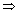 |
|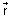 |2 - (
|2 - (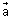 +
+ 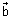 ).
).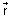 +
+ 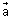 .
.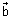 = 0
= 0 or AP2 + BP2 = AB2
|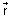 - - 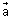 |2 + | |2 + |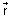 - - 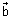 | = | | = |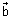 - - 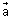 |2 |2 |
Cartesian Form: If A(x1, y1, z1) & B(x2, y2, z2) are extremities of diameter then, eq. of sphere is (x - x1)(x - x2) + (y - y1)(y - y2) + (z - z1)(z - z2) = 0
Section of sphere by plane:
If sphere is intersection by a plane. We get circle by intersection.
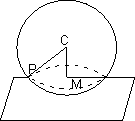
PM is radius of circle
PM =
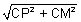
Condition of Tangency of plane to a sphere:
Vector Form: Plane
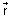 .
.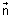 = d touches sphere |
= d touches sphere |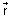 -
- 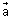 | = R
| = R if
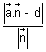 = R
= R Dumb Question: Why
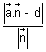 = R ?
= R ? Ans: A plane touches to sphere if
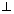 distaqnce from centre of sphere is equal to radius.
distaqnce from centre of sphere is equal to radius.Cartesian Form: Plane ln + my + nz = p touches (ul + vm + wn + p)2 = (l2 + m2 + n2)(u2 + v2 + w2 -d)
Illustration: Find eq. of sphere whose centre has P.V.
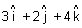 & which touches plane
& which touches plane 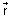 .
.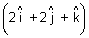 = 10
= 10 Ans: Center =
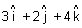
It touches plane
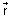 .
.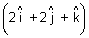 = 10
= 10 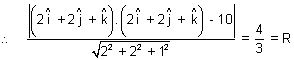
 eq. of sphere |
eq. of sphere |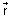 -
- 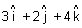 | =
| = 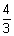
Easy Type
Q.1. Find ratio in which 2x + 3y + 5z = 1 divides line joining the points (1, 0, 2) & (1, 2, 5)
Ans: Let the ratio be k = 1 at point P
Then, P =
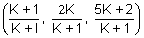 must satisfy 2x + 3y + 5z = 1
must satisfy 2x + 3y + 5z = 1 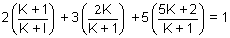
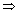 2(K + 1) + 6K + 25K + 10 = K + 1
2(K + 1) + 6K + 25K + 10 = K + 1 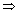 K + 1 + 6K + 25K + 10 = 0
K + 1 + 6K + 25K + 10 = 0 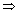 32K + 11 = 0
32K + 11 = 0 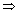 K =
K = 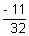
Thus line divides externally in rstio of 11:32