3D Geometry - 6
Introduction
Q.2. What are direction cosines of a line which is equally inclined to axes ?Ans: If
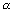 ,
, 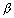 ,
, 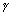 are angles, if line is equally inclined
are angles, if line is equally inclined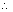
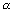 =
= 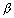 =
= 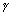
l2 + m2 + n2
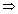 cos2
cos2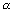 + cos2
+ cos2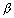 + cos2
+ cos2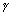 = 1
= 1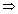 3 cos2
3 cos2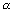 = 1
= 1 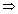 cos
cos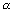 = ±
= ± 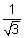 = cos
= cos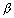 = cos
= cos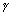
 d.c's arw (
d.c's arw (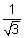 ,
, 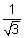 ,
, 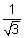 ) or (-
) or (- 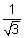 , -
, - 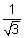 , -
, - 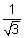 )
)Q.3. Find direction cosines of line which is
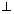 to lines with d.r (1, -2, -2) & (0, 2, 1)
to lines with d.r (1, -2, -2) & (0, 2, 1)Ans: Let l, m, n be d.c's line 1 to given line, d.c's are proportional to d.r's
 d.c'r of lines are (
d.c'r of lines are ( , - 2
, - 2 , - 2
, - 2 ) & (0, 2µ, µ)
) & (0, 2µ, µ)Since line is
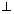 to given lines
to given linesl
 + (- 2m
+ (- 2m ) + (- 2n
) + (- 2n ) = 0
) = 0 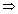 l - 2m - 2n = 0
l - 2m - 2n = 0& 0 + 2mµ + nµ = 0
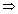 2m + n = 0
2m + n = 0By cross multiplication,
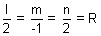
l = 2R, m = - R & n = 2R
l2 + m2 + n2 = 1
4R2 + R2 + 4R2 = 1
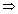 9R2 = 1
9R2 = 1 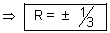
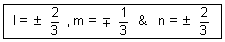
Q.4. Prove that line x = ay + b, z = cy + d & x = a'y + b', z = c'y + d' are
 if aa' + cc' + 1 = 0
if aa' + cc' + 1 = 0Ans: Ist line is x = ay + b, z = cy + d
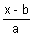 = y,
= y, 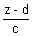 = y
= y 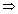
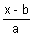 =
= 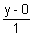 =
= 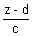 ................................ (i)
................................ (i)and IInd line
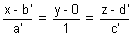 ................................................. (ii)
................................................. (ii)These lines are
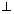 if
ifaa' + |x| + cc' = 0
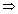 aa' + cc' + 1 = 0
aa' + cc' + 1 = 0Dumb Question: For what value of k, lines
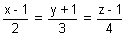 &
& 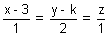 intersect?
intersect?Ans:
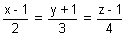 =
= 
and
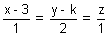 = µ
= µSince these lines have point of intersection in common. then
(2
 + 1, 3
+ 1, 3 - 1, 4
- 1, 4 + 1) = (µ + 3, 2µ + k, µ)
+ 1) = (µ + 3, 2µ + k, µ)or 2
 + 1 = µ + 3 ....... (i), 3
+ 1 = µ + 3 ....... (i), 3 - 1 = 2µ + k ....... (ii) & 4
- 1 = 2µ + k ....... (ii) & 4 + 1 = µ ....... (iii)
+ 1 = µ ....... (iii)on solving (i) & (iii), we get
 = - 3/2 & µ = - 5
= - 3/2 & µ = - 5Substituting in (ii)
-
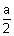 - 1 = - 10 + k
- 1 = - 10 + k 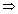 k =
k = 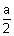
Q.6. Show that points
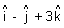 and
and 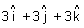 are equidistant from plane
are equidistant from plane 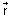 .(
.(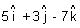 ) + 9 = 0
) + 9 = 0Ans:
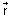 .(
.(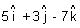 ) = - 9
) = - 9length of
 from (
from (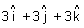 )
)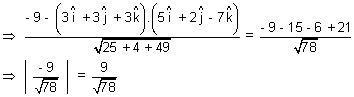
So, length of
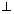 is equal.
is equal.Q.7. Find the point in which the plane;
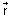 = (
= (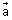 -
-  ) + m(
) + m(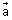 +
+  +
+ 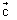 ) + n(
) + n(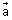 +
+ 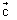 -
-  ) is cut by line through point 2
) is cut by line through point 2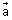 + 3
+ 3 & parallel to
& parallel to 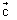 .
.Ans: eq. of line through point 2
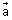 + 3
+ 3 & || to
& || to 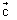
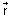 = (2
= (2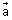 + 3
+ 3 ) +
) + 
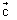
Since line cuts plane
For one point,
(2
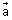 + 3
+ 3 ) +
) + 
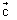 =
= 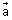 -
-  + m(
+ m(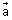 +
+  +
+ 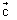 ) + n(
) + n(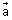 +
+ 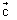 -
-  )
)Equating coeff. of
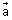 ,
,  &
& 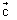 on both side, we get
on both side, we getm + n = 1, m - n = 4, - m + n =

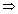 m =
m = 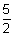 , n =
, n = 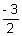 &
&  = - 4
= - 4 P.V. of required point is: 2
P.V. of required point is: 2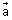 + 3
+ 3 - 4
- 4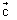
Q.8. Show that line of intersection of planes
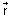 .(
.(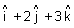 ) = 0 &
) = 0 & 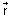 .(
.(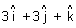 ) = 0 is equally inclined to
) = 0 is equally inclined to 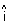 &
& 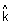 .
.Ans: Note: Line of intersection of two planes will be
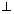 to normals to the planes. Hence it is || to vector
to normals to the planes. Hence it is || to vector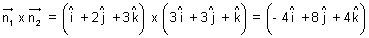
Now,
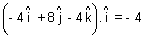
&
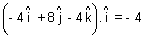
So, line is equally inclined to
 &
& 
Q.9. Projection of line segment on 3 axes 4, 5 & 13 respectively. Find length & direction cosines of line segment.
Ans:
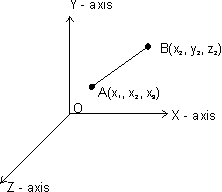
 = (x2 - x1)
= (x2 - x1) + (y2 - y1)
+ (y2 - y1) + (z2 - z1)
+ (z2 - z1)
 Projection of
Projection of 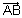 on x-axis
on x-axis=
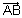 .
.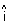 = (x2 - x1) = 4
= (x2 - x1) = 4Projection of
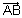 on y-axis
on y-axis=
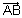 .
.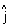 = (y2 - y1) = 5
= (y2 - y1) = 5Projection of
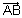 on z-axis
on z-axis=
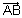 .
.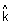 = (z2 - z1) = 13
= (z2 - z1) = 13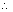 Length of AB =
Length of AB = 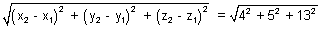
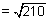
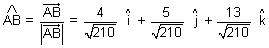
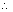 d.r's =
d.r's = 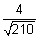 ,
, 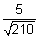 &
& 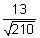
Q.10. Find locus of mid point of chords of sphere r2 - 2
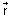 .
.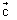 + k = 0 if chords being drawn || to vector
+ k = 0 if chords being drawn || to vector  .
.Ans: r2 - 2
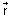 .
.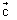 + k = 0 is sphere of centre
+ k = 0 is sphere of centre 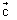 chord AB ||
chord AB ||  .
.
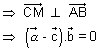
 locus of M is (
locus of M is (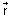 -
- 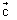 ).
). = 0
= 0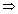
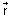 .
. =
= 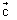 .
.
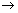 represents a plane.
represents a plane.Dumb Question: Why
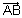 is same as
is same as 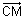
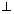
 ?
?Ans: Since
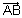 ||
||  . So, if
. So, if  is
is 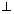
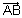 . So, it will also
. So, it will also  to
to  .
.Medium Type
Q.1. If a variable plane forms a tetrahedron of constant volume 27k3 with coordinate planes, find locus of centroid of tetrahedron.
Ans: sLet variable plane cuts coordinate axes at A(a, 0, 0), B(0, b, 0), C(0, 0, c)
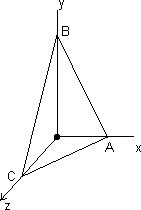
Then, eq. of plane will be
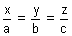 = 1
= 1Let P
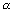 ,
, 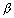 ,
, 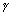 ) be centroid of terahedron OABC,
) be centroid of terahedron OABC,then,
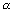 =
= 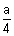 ,
, 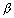 =
= 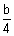 ,
, 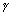 =
= 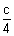
[Dumb Question: How this centroid tetrahedron OABC comes
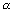 =
= 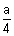 ,
, 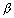 =
= 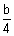 ,
, 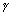 =
= 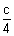 ?
?Ans: Centroid of tetrahedrold
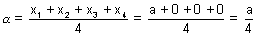
where (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) & (x4, y4, z4) are coordinate of tetrahedron.]
Volume of tetrahedron =
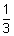 (Area of
(Area of 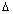 AOB).OC
AOB).OC27k3 =
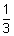 (
(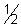 ab)c =
ab)c = 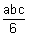
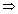 27k3 =
27k3 = 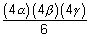
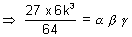
Required locus of P(
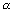 ,
, 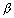 ,
, 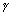 ) is
) is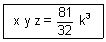
Q.2. Find vector eq. of straight line passing through intersection of plane
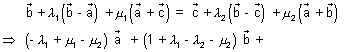
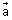 ,
,  ,
, 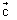 are non coplanar vectors.
are non coplanar vectors.Ans: At points of intersection of two planes.
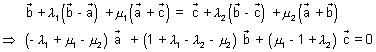
Since
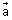 ,
,  ,
, 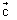 are non coplanar, then
are non coplanar, then-
 1 + µ1 - µ2 = 0, 1 +
1 + µ1 - µ2 = 0, 1 +  1 -
1 -  2 - µ2 = 0, µ1 - 1 +
2 - µ2 = 0, µ1 - 1 +  2 = 0
2 = 0