3D Geometry - 7
On solving, we get 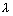 1 = 0 & µ1 = µ2
1 = 0 & µ1 = µ2
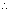
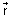 =
=  +
+ 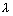 1(
1( -
-  ) + µ1(
) + µ1( +
+  )
)
Since 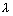 1 = 0
1 = 0

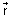 =
=  + µ1(
+ µ1( +
+  ) is required eq. of straight line.
) is required eq. of straight line.
Q.3. Prove that three lines from O with direction cosines l1, m1, n1; l2, m2, n2; l3, m3, n3 are coplaner if
l1(m2n3 - n2m3) + m1(n2l3 - l2n3) + n1(l2m3 - l3m2) = 0
Ans: Note: Three given lines are coplanar if they have common perpendicular. Let d.c’s of common 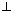 be l, m, n
be l, m, n
 ll1 + mm1 + nn1 = 0 ……………………….. (i)
ll1 + mm1 + nn1 = 0 ……………………….. (i)
ll2 + mm2 + nn2 = 0 ……………………….. (ii)
ll3 + mm3 + nn3 = 0 ……………………….. (iii)
Soplving (ii) & (iii) by cross multiplication ……


l = k(m2n3 - n2m3), m = k(n2l3 - n3l2), n = k(l2m3 - l3m2)
Substituting in (i), we get
k(m2n3 - n2m3)l1 + k(n2l3 - n3l2)m1 + k(l2m3 - l3m2)n1 = 0
 l1(m2n3 - n2m3) + m1(n2l3 - n3l2) + n1(l2m3 - l3m2) = = 0
l1(m2n3 - n2m3) + m1(n2l3 - n3l2) + n1(l2m3 - l3m2) = = 0
Q.4. Solve the equation x + y
+ y + z
+ z =
= 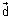
Ans: x + y
+ y + z
+ z =
= 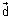 ……………………………. (i)
……………………………. (i)
Taking dot product by  x
x  , we get
, we get
x .(
.( x
x  ) + y
) + y .(
.( x
x  ) + z
) + z .(
.( x
x  ) =
) = 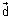 .(
.( x
x  )
)
x[

 ] = [
] = [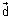

 ]
]  x =
x = 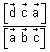
& z = 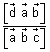
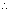 x
x + y
+ y + z
+ z =
= 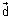
 [
[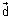

 ]
] + [
+ [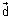

 ]
] + [
+ [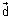

 ]
] = [
= [

 ]
]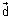 is required solution.
is required solution.
Q.5. If planes x - cy - bz = 0, cx - y + az = 0 & bx + ay - z = 0 pass through a straight line, the find value of a2 + b2 + c2 + 2abc.
Ans: Givem planes are:
x - cy - bz = 0 ……………………….. (i)
cx - y + az = 0 ……………………….. (ii)
& bx + ay - z = 0 ……………………….. (iii)
Eq. of plane passing through line of intersection of plane (i) & (ii) is
(x - cy - bz) + 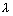 (cx - y + az) = 0
(cx - y + az) = 0
 x(1 +
x(1 + 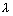 c) -
c) - 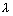 (c +
(c + 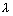 ) + z(- b + a
) + z(- b + a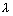 ) = 0 ……………………….. (iv)
) = 0 ……………………….. (iv)
If plane (iv) & (iii) are same, then,
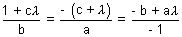
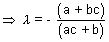 and
and 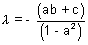
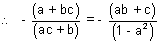
 a - a3 + bc - a2bc = a2bc + ac2 + ab2 + bc
a - a3 + bc - a2bc = a2bc + ac2 + ab2 + bc
 a(2abc + c2 + b2 + a2 - 1) = 0
a(2abc + c2 + b2 + a2 - 1) = 0
 a2 + b2 + c2 + 2abc = 1
a2 + b2 + c2 + 2abc = 1
Q.1. Show that
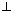 distance of a point A(
distance of a point A( ) to line
) to line 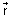 =
=  + t
+ t is
is  which is also equal to
which is also equal to 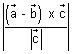 .
. Ans:
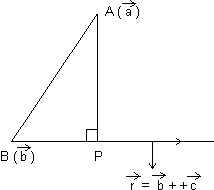
Let P is point on line such that
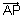
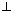
 & P.V. of P is
& P.V. of P is 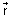 =
=  + t
+ t
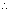
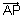 .
.  = 0
= 0 (
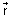 -
-  ).(
).(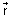 -
-  ) = 0 ……………………… (i)
) = 0 ……………………… (i)(
 + t
+ t -
-  ).(
).( + t
+ t -
-  ) = 0
) = 0 (
 -
-  + t
+ t ).(t
).(t ) = 0
) = 0  t
t .
. - t
- t
 + t2
+ t2
 = 0
= 0  t
t (
( -
-  ) + t2c2 = 0
) + t2c2 = 0  t =
t =  ………………………………. (ii)
………………………………. (ii) From (i) & (ii)
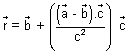
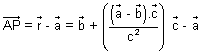
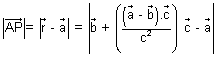 ………………………………… (iii)
………………………………… (iii) Also, PA2 = AB2 - BP2 = |
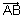 |2 - |
|2 - | |2
|2
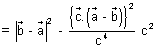
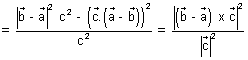 ………………………………… (iv)
………………………………… (iv) Dumb Question: How this eq. (iv) const.
Ans: We know that (AB)2 -
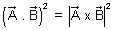
Q.2. If direction cosines of variable line in two adjacent points be l, m, n & l +
 l, m +
l, m +  m, n +
m, n +  n show that small anhgle 5
n show that small anhgle 5 b/w two position is
b/w two position is 
 2 =
2 =  l2 +
l2 +  m2 +
m2 +  n2
n2Ans: As we know l2 + m2 + n2 = 1
and (l +
 l)2 + (m +
l)2 + (m +  m)2 + (n +
m)2 + (n +  n)2 = 1
n)2 = 1  l2 + (
l2 + ( l2) 2l
l2) 2l l + m2 + (
l + m2 + ( m)2 + 2m
m)2 + 2m m + n2 + (
m + n2 + ( n)2 + 2n
n)2 + 2n n = 1
n = 1  l2 + m2 + n2 + (
l2 + m2 + n2 + ( l)2 + (
l)2 + ( m)2 + (
m)2 + ( n)2 + 2(l
n)2 + 2(l l + m
l + m m + n
m + n n) = 1
n) = 1  (
( l)2 + (
l)2 + ( m)2 + (
m)2 + ( n)2 = - 2(l
n)2 = - 2(l l + m
l + m m + n
m + n n) ………………………. (i)
n) ………………………. (i) 
 is angle b/w two positions.
is angle b/w two positions. cos

 = l(l +
= l(l +  l) + m(m +
l) + m(m +  m) + n(n +
m) + n(n +  n)
n) 1 - 2 sin2
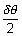 = 1 + l
= 1 + l l + m
l + m m + n
m + n n ……………………………………. (ii)
n ……………………………………. (ii) From (i) & (ii)
(
 l)2 + (
l)2 + ( m)2 + (
m)2 + ( n)2 = 4 sin2
n)2 = 4 sin2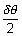
 4(
4(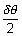 )2 = (
)2 = ( l)2 + (
l)2 + ( m)2 + (
m)2 + ( n)2
n)2 (  )2 = ( )2 = ( l)2 + ( l)2 + ( m)2 + ( m)2 + ( n)2 n)2 |
Dumb Question: How sin2
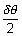 is equal to (
is equal to (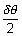 )2 ?
)2 ? Ans: Since

 is very small so,
is very small so, 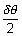 is very small
is very small So, sin
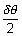
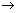
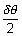 as
as 

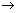 0
0 So, for approsmation we have taken.
Q.3. Find image of point P(3, 5, 6) in plane 2x + y + z = 0 & find eq. of sphere having point P(3, 5, 6) & its image point of extremities of diameter.
Ans:
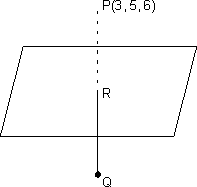
2x + y + z = 0
P(3, 5, 6)
dr’s iof normal to plane (i) are 2, 1, 1
Let
 be image of point P in plane (i)
be image of point P in plane (i) Eq of P R is,
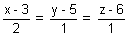 = r
= r  R(2r + 3, r + 5, r + 6)
R(2r + 3, r + 5, r + 6) [Dumb Question: How eq. of line PR come ?
Ans: d.r’s of normal to plane is same as d.r’s of line PR i.e. 2, 1, 1
So, we get eq. of line PR]
But R lies on (i)
 2(2r + 3) +(r + 5) + (r + 6) = 0
2(2r + 3) +(r + 5) + (r + 6) = 0 6r + 17 = 0
 r = -
r = - 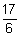
R

Since R lies mid point of PQ
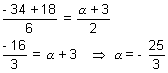
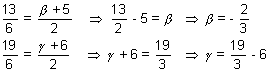
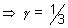
Q =
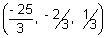
Eq. of sphere when extremities (x1, y1, z1) & (x2, y2, z2) are given:
(x - x1)(x - x2) + (y - y1)(y - y2) + (z - z1)(z - z2) = 0
(x - 3)
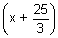 + (y - 5)
+ (y - 5)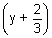 + (z - 6)
+ (z - 6)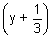 = 0
= 0  x2 + y2 + z2 +
x2 + y2 + z2 +  = 0
= 0 x2 + y2 + z2 +
x2 + y2 + z2 + 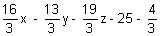 = 0
= 0 3x2 + 3y2 + 3z2 + 16x - 13y - 19z - 79 = 0
3x2 + 3y2 + 3z2 + 16x - 13y - 19z - 79 = 0 Key words
 Direction COsines.
Direction COsines.  Direction Ratios.
Direction Ratios. Reflection of a point.
Reflection of a point.  Skew Lines.
Skew Lines.  Shortest distance.
Shortest distance.  Intersection of lines.
Intersection of lines.  Normal. FV
Normal. FV Angle bisector.
Angle bisector.  Tangency of plane to sphere.
Tangency of plane to sphere.