application-of-derivatives-4
Increasing function:
(a) Strictly increasing function:
A function f(x) is c/d strictly increasing function in its domain if x1 < x2
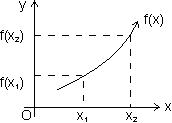
For strictly increasing function f'(x) > 0v x 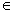 domain
domain
Dumb Question: How f'(x) > 0nv x 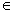 domain for strictly increasin function.
domain for strictly increasin function.
Ans: As x1 < x2
 f(x1) < f(x2)
f(x1) < f(x2)
So, f(x) < f(n + h)
f'(x) =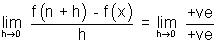
 f'(x) > 0
f'(x) > 0
Types of strictly increasing function:
(1) Concave up: When f'(x) > 0 & f"(x) > 0v x  domain
domain
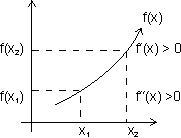
(2) Concave down: f'(x) > 0 & f"(x) < 0v x  domain
domain
(3) When f'(x) > 0 & f"(x) = 0v x  domain
domain
f'(x)> 0 & f"(x) = 0
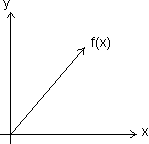
Increasing function:
A function f(x) is said to be non decreasing if for x1 < x2
Laet us see in fig.
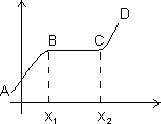
For portion ABCD, x1 < x2
 f(x1) < f(x2)
f(x1) < f(x2)
 for BC, x1 < x2
for BC, x1 < x2
 f(x1) = f(x2)
f(x1) = f(x2)
Dumb Question: What is diff. b/w strictly increasing & increasing function ?
Ans: Strictly function for x1 < x2, f(x2) is always greater than f(x1) but in increasing function for x1 < x2, f(x2 may be greater or equal to f(x1).
Decreasing functions:
(a) Strictly decreasing function:
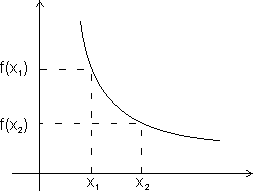
A function f(x) ic c/d strictly decreasimg in its domain if x1 < x2
 f(x1) > f(x2)
f(x1) > f(x2)
For strictly decreasing function.
f'(x) < 0
Dumb Question: How f'(x) < 0 for strictly decreasing ?
Ans: As x1 < x2 f(x1) > f(x2)
f(x1) > f(x2)
So, f(x + h) < f(x)
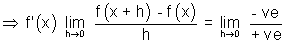
 f'(x) < 0
f'(x) < 0
Types of strictly decreasing function:
(i) Concave up:
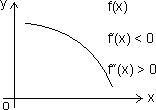
When f'(x) < 0
 f''(x) > 0
f''(x) > 0 v x  domain
domain
(ii) Concave down:
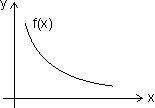
When f'(x) < 0 & f''(x) < 0v x 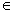 domain
domain
(iii)

When f'(x) < 0 & f'(x) = 0v x 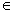 domain
domain
(5) Non-increasing function:
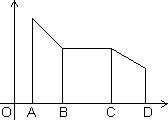
A function f(x) is c/d non-increasing if for x1 < x2
for x1 < x2
 f(x1)
f(x1) 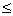 f(x2)
f(x2)
For AB & CD, x1 < x2
 f(x1 > f(x2)
f(x1 > f(x2)
Bc, x1 < x2
 f(x1 = f(x2)
f(x1 = f(x2)
Illustration: Find interval in which f(x) = x3 - 3x2 - 9x + 20 is strictly increasing or decreasing.
Ans: f(x) = x3 - 3x2 - 9x + 20
f'(x) = 3x2 - 6x - 9
 f'(x) = 3(x - 3)(x + 1)
f'(x) = 3(x - 3)(x + 1)
For strictly increasing
f'(x) > 0
 3(x - 3)(x + 1) > 0
3(x - 3)(x + 1) > 0  (x - 3)(x + 1) > 0
(x - 3)(x + 1) > 0
 (x + 1) < 0 or (x - 3) > 0
(x + 1) < 0 or (x - 3) > 0
 x < - 1 or x > 3
x < - 1 or x > 3
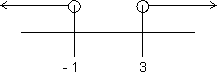
x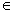 (-
(- 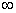 , - 1) U (3,
, - 1) U (3, 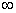 )
)
For strictly decreasing
f'(x) < 0
(x + 1)(x - 3) < 0
 x
x 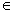 (- 1, 3)
(- 1, 3)
(a) Strictly increasing function:
A function f(x) is c/d strictly increasing function in its domain if x1 < x2
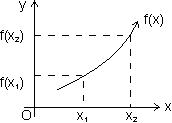
For strictly increasing function f'(x) > 0
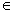 domain
domainDumb Question: How f'(x) > 0n
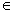 domain for strictly increasin function.
domain for strictly increasin function.Ans: As x1 < x2
 f(x1) < f(x2)
f(x1) < f(x2)So, f(x) < f(n + h)
f'(x) =
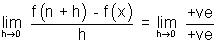
 f'(x) > 0
f'(x) > 0Types of strictly increasing function:
(1) Concave up: When f'(x) > 0 & f"(x) > 0
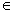 domain
domain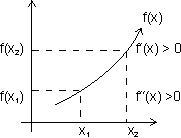
(2) Concave down: f'(x) > 0 & f"(x) < 0
 domain
domain
(3) When f'(x) > 0 & f"(x) = 0
 domain
domainf'(x)> 0 & f"(x) = 0
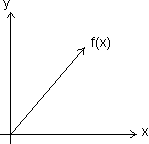
Increasing function:
A function f(x) is said to be non decreasing if for x1 < x2
Laet us see in fig.
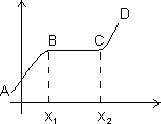
For portion ABCD, x1 < x2
 f(x1) < f(x2)
f(x1) < f(x2) for BC, x1 < x2
for BC, x1 < x2 f(x1) = f(x2)
f(x1) = f(x2)Dumb Question: What is diff. b/w strictly increasing & increasing function ?
Ans: Strictly function for x1 < x2, f(x2) is always greater than f(x1) but in increasing function for x1 < x2, f(x2 may be greater or equal to f(x1).
Decreasing functions:
(a) Strictly decreasing function:
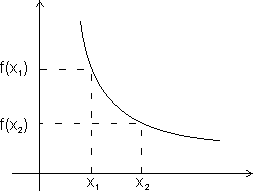
A function f(x) ic c/d strictly decreasimg in its domain if x1 < x2
 f(x1) > f(x2)
f(x1) > f(x2)For strictly decreasing function.
f'(x) < 0
Dumb Question: How f'(x) < 0 for strictly decreasing ?
Ans: As x1 < x2
 f(x1) > f(x2)
f(x1) > f(x2)So, f(x + h) < f(x)
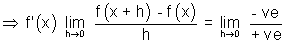
 f'(x) < 0
f'(x) < 0Types of strictly decreasing function:
(i) Concave up:
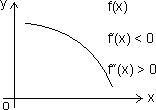
When f'(x) < 0
 f''(x) > 0
f''(x) > 0  domain
domain(ii) Concave down:
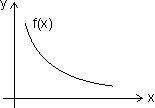
When f'(x) < 0 & f''(x) < 0
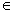 domain
domain(iii)

When f'(x) < 0 & f'(x) = 0
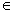 domain
domain(5) Non-increasing function:

A function f(x) is c/d non-increasing if for x1 < x2
for x1 < x2
 f(x1)
f(x1) 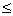 f(x2)
f(x2)For AB & CD, x1 < x2
 f(x1 > f(x2)
f(x1 > f(x2)Bc, x1 < x2
 f(x1 = f(x2)
f(x1 = f(x2)Illustration: Find interval in which f(x) = x3 - 3x2 - 9x + 20 is strictly increasing or decreasing.
Ans: f(x) = x3 - 3x2 - 9x + 20
f'(x) = 3x2 - 6x - 9
 f'(x) = 3(x - 3)(x + 1)
f'(x) = 3(x - 3)(x + 1)For strictly increasing
f'(x) > 0
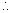 3(x - 3)(x + 1) > 0
3(x - 3)(x + 1) > 0  (x - 3)(x + 1) > 0
(x - 3)(x + 1) > 0 (x + 1) < 0 or (x - 3) > 0
(x + 1) < 0 or (x - 3) > 0 x < - 1 or x > 3
x < - 1 or x > 3
x
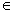 (-
(- 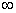 , - 1) U (3,
, - 1) U (3, 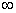 )
)For strictly decreasing
f'(x) < 0
(x + 1)(x - 3) < 0
 x
x 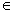 (- 1, 3)
(- 1, 3)