Properties of Monotonic function:
(1) If f(x) is strictly increasing function on [a, b]
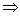
{ f'(x) exists & f'(x) is also strictly increasing on [a, b].
(2) If f(x) & g(x) are also two continous & differentiable functions & fog(x) & gof(x) exists . then,

In other words
(i) If f(x) & g(x) are both strictly increasing or strictly decreasing.
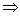
(fog)(x) & (gof)(x) both are strictly inctreasing.
(ii) If amongst two functions f(x) & g(x), one is strictly increasing other is strictly decreasing.
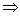
(fog)(x) & (gof)(x) both are strictly decreasing.
Illustration: Let Ø(x) = sin(cosx) then check it whethe5r increasing ordecreasing in [0,
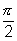
].
Ans: Ø(x) will be increasing if Ø'(x) > 0
Ø(x) = sin(cosx)
Ø'(x) = cos(cosx).(- sinx)
So, it is clearly decreasing for x
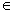
[0,
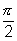
] as Ø'(x)

0
Other method: f(x) = sinx & I(x) = cosx are increasing & decreasing in [0,
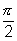
]
fog(x) = Ø(x) = sin(cosx) is decreasing.
Critical Points:
It is collection of points for which,
(i) f(x) does not exists.
(ii) f'(x) does not exists.
(iii) f'(x) = 0
All values of x obtained from above conditions are c/d critical points.
Illustration: Find critical points for f(x) = (x - 2)
2/3(2x + 1)
Ans: f(x) = (x - 2)
2/3(2x + 1)
f'(x) =
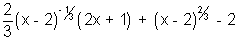
f'(x) =

Clearly f'(x) doesnot defined at x = 2 so, x = 2 is critical point.
Dumb Question: Why f'(x) is not defined at x = 2 ?
Ans: Putting x = 2, f'(x) =
which is not defined.
Another critical point
f'(x) = 0

= 0
x = 1
So, x = 1 & x = 2 are two critical points of f(x)
Maxima & Minima:
Maxima: A function f(x) is said have maxima at x = a if f(a)

f(a + h) where h

0 (very small & a lies in its domain.
Minima: A function f(x) is said to have minima at x = b if f(b)

f(b + b) & f(b)

f(b - b) where h

0 (very small)
Methods for finding extremum of continuone functions:
(a)
First derivative test:
(i)
When f(x) attains maximum at x = a:
From graph,
For x < a,
 1
1 < 90
0 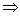
tan
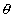 1
1 > 0 or increasing for x < a
For x = a, tan
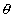
= 0 or neither increasing nor decreasing for x = a.
For x > a,
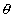 2
2 > 90
0 
tan
 2
2 < 0 or decreasing for x > a
So,
f(x) is maximum at x =a
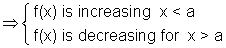
(ii)
When f(x) attains minimum at x = b:
From graph,
For x < b,
 1
1 > 90
0 tan
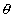 1
1 < 0 or decreasing when x - < b
For x = b, tan
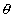
= 0 or neither increasing nor decreasing for x = b
For x > b,
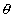 2
2 < 90
0 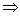
tan
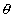 2
2 > 0 or increasing when x > b
So,
f(x) is minimum at x = b
 Illustration
Illustration: Let f(x) = x
3 - 3x
2 + 6, find point at which f(x) have local maximum & local minimum.
Ans: f(x) = x
3 - 3x
2 + 6
f'(x) = 3x
2 - 6x
Critical points are if f'(x) = 0
3x
2 - 6x = 0
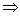
x
2 - 2x = 0
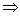
x = 0, 2
At x = 0, f'(x) change sign from + ve to - ve & f'(x) changes sign from - ve to + ve at x = 2.
So, at x = 0, function has local maxima 7 at x = 2 it has local minima.
Second Derivative Test:
(1) First we find root of f'(x) = 0.
Let x = a is one roots of f'(x) = 0
(2) Now find f''(x) at x = a
(i) If f''(a) = -ve, then f(x) is max. at x = a.
(ii) If f''(a) = +ve, then f(x) is min. at x = a
(iii) If f''(a) = 0
Then find F'''(x) at x = 0
If f'''(a)
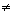
= 0 then f(x) has neither maximum nor minimum at x = a.
But if f'''(a) = + ve, then find f'
v(a),
(a) If f'
v = + ve, then f(x) is min. at x = a.
(b) If f'
v(a) = - ve, then f(x) is max. at x = a.