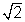application-of-derivatives-6
Illustration: Let f(x) = x(x - 1)2, find point at which f(x) have maxima & minima.
Ans: f(x) = x(x - 1)2
f’(x) = 2x(x - 1) + (x - 1)2
f’(x) = (x - 1)(3x - 1)
f’(x) = 0
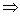 (x - 1)(3x - 1) = 0
(x - 1)(3x - 1) = 0
 Critical points are x = 1, 1⁄3
Critical points are x = 1, 1⁄3
f”(x) = 6x - 4
 f”(1) = 6 - 4 = 2 > 0
f”(1) = 6 - 4 = 2 > 0
 f”(-1⁄3) = - 2 < 0
f”(-1⁄3) = - 2 < 0
f”(1) > 0 so, at n = 1 it has minima
f”(1⁄3) < 0 so, maxima at x = 1⁄3.
Global Maxima & Minima:
(i) Global maxima/minima in [a, b] is a greatest/least value of f(x) in [a, b]
Global maxima/minima in [a, b] would always occur at critical points of f(x) with in [a,b] or end points of interval.
To find global maxima/minima of f(x) in [a, b] find out all critical points of f(x) in a, b = 0)
Let c1, c2, ………. cn be critical points & f(c1), f(c2), ………….. f(cn) be values of function of these points.
Let M1  Global Maxima
Global Maxima
M2  Global Minima
Global Minima
Then M1 = max.{f(a), f(c1), f(c2), …………… f(cn), f(b)}
& M2 = min.{f(a), f(c1), f(c2), ……………. f(cn), f(b)}
Illustration: If f(x) = 2x3 - 9x2 + 12x + 6. Discuss global maxima and minima of f(x) in (1, 3).
Ans: f(x) = 2x3 - 9x2 + 12x + 6
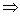 f’(x) = 6x2 - 18x + 12
f’(x) = 6x2 - 18x + 12
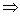 f’(x) = 6(x - 1)(x - 2)
f’(x) = 6(x - 1)(x - 2)
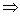 f’(x) = 0
f’(x) = 0 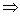 x = 1, 2
x = 1, 2
 f(1) = 11 & 1 - (2) = 10
f(1) = 11 & 1 - (2) = 10
Since open interval is (1, 3)
Clearly x = 2 is only point in (1, 3) & 1 - (2) = 10
Now, 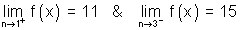
Dumb Question: How 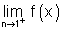 = 11.
= 11.
Ans: f(x) = 2x2 - 9x2 + 12x + 6
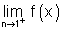 =
=  f(1 + h)
f(1 + h)
=  2(1 + h)3 - 9(1 + h)2 + 12(1 + h) + 6
2(1 + h)3 - 9(1 + h)2 + 12(1 + h) + 6
=  2(1 + h3 + 3h2 + 3h) - 9(1 + h2 + 2h) + 12 + 12h + 6
2(1 + h3 + 3h2 + 3h) - 9(1 + h2 + 2h) + 12 + 12h + 6
= 11
So, x = 2 is point of global minima in (1, 3) & global maxima doesnot exist in (1, 3) .
Minima of discontinuous function:
For minima at x = a, 4 cases arises.

From figure f(CD) < f(a + h) From figure f(a) < f(a + h)
f(a) < f(a - h) f(a)
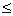 f(a - h)
f(a - h) 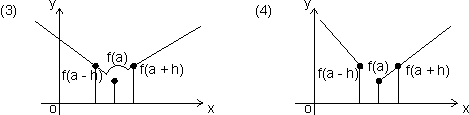
From figure, f(a) < f(a + h) From figure, f(a)
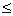 f(a + h)
f(a + h) f(a) < f(a - h) f(a) < f(a - h)
From all above case, for minima of discontinuous functions,
f(a)
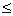 f(a + h)
f(a + h) 2f(a)
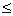 f(a - h)
f(a - h) Illustration: Discuss minima of f(x) = {x}, (where {} is raction part of x) for x = 6.
Ans: For discont functions, maximum & minimum at x = a is attained when
f(a)
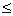 f(a + h) & f(a)
f(a + h) & f(a) 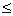 f(a - h)
f(a - h) Now, f(x) = {x} is discontinuous function at x = 6
Since f© = {6} = 0
f(6 + h) = {6 + h} = h > 0
& f(6 - h) = {6 - h} = 1 - h > 0
So, f(6) < f(6 + h) & f(6) < f(6 - h)
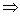 f(x) is minimum at x = 6.
f(x) is minimum at x = 6. Dumb Question: How f(6) = {6} = 0
Ans: {x} is fractional function. Since6 is integer & no fractional part
 f(6) = 0
f(6) = 0 Maxima of discontinuous function:
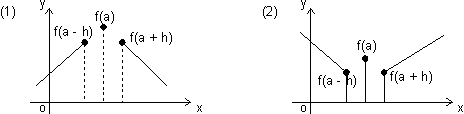
From figure, f(a) > f(a + h) From figure, f(a) > f(a + h)
f(a) > f(a - h) f(a) > f(a - h)
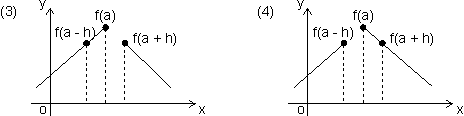
From figure, f(a)
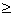 f(a - h) From figure, f(a)
f(a - h) From figure, f(a) 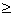 f(a + h)
f(a + h) f(a) > f(a + h) f(a) > f(a - h)
Prove all cases, maxima of discontinuous function,
f(a)
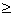 f(a + h) & f(a)
f(a + h) & f(a) 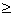 f(a - h)
f(a - h) Illustration: f(x) =
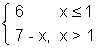 , then for f(x) at x = 1 discuss maxima & minima.
, then for f(x) at x = 1 discuss maxima & minima. Ans:
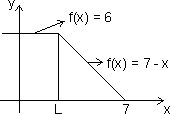
f(x) =
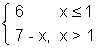
 f(1) = 6
f(1) = 6 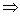 f(1 - h) = 6
f(1 - h) = 6 & f(1 + h) = 7 - (1 + h) = 6 - h < 6
So, at x = 1 is neither point of maxima nor manima.
Easy Type:
Q.1. If s = t3 - 4t, find acceleration at time when velocity is zero.
Ans: s = t3 - 4t
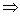 v =
v =  = 3t2 - 4 …………………………………………. (i)
= 3t2 - 4 …………………………………………. (i) a =
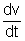 = 6t ………………………………………………. (ii)
= 6t ………………………………………………. (ii)time at which velocity is zero
3t2 - 4 = 0
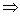 t2 =
t2 = 
a =
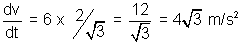
Q.2. If r be radius, s the surface atrea & v the volume of spherical buble, prove that
(i)
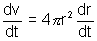 (ii)
(ii) 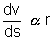
Since v =
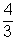
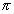 r3
r3 (i)
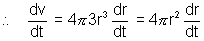 ……………………………. (i)
……………………………. (i) (ii) s = 4
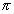 r2
r2 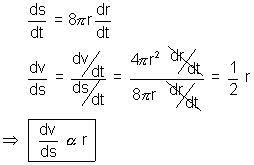
Q.3. On curve x3 = 12y, find interval at which abscissa changes at a faster rate than ordinate.
Ans: x3 = 12y
differencing w.r.t. y
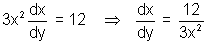
Since abscissa change faster than ordinate
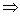
 > 1 or
> 1 or 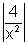 > 1
> 1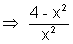 > 0 where x
> 0 where x 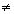 0
0 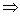 x2 - 4 < 0
x2 - 4 < 0 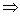 (x - 2)(x + 2) < 0
(x - 2)(x + 2) < 0 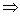 - 2 < x < 2
- 2 < x < 2 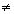 {0}
{0} So, x
 (- 2, 2) - {0} is required interval.
(- 2, 2) - {0} is required interval. Q.4. Find eq. of tangent to parabola y2 = 4ax at point (at2, 2at)
Ans: y2 = 4ax …………………………………………………… (i)
differentiating (i) w.r.t. x,

Eq. of tangent at (at2, 2at) is
(y - 2at) =

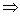 y - 2at =
y - 2at = 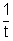 (x - at2)
(x - at2) 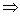 yt = x + at2 yt = x + at2 |
Q.5. Find a cute angle b/w curves y = |x2 - 1| & y = |x2 - 3| at their points of intersection when x > 0.
Ans: For intersection of given curves
|x2 - 1| = |x2 - 3|
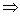 (x2 - 1)2 = (x2 - 3)2
(x2 - 1)2 = (x2 - 3)2 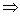 2x2 = 4
2x2 = 4 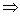 x = ±
x = ±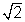
Since x > 0, so, x =
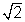 is only point of intersection
is only point of intersection y = |x2 - 1| = (x2 - 1) since x =
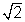
y = |x2 - 3| = - (x2 - 3) since x =