application-of-derivatives-7
Dumb Question: How y = |x2 - 3| = - (x2 - 3) for neighbour hood of x = 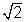 .
.
Ans: y = |x2 - 3| since |x2 - 3| is + ve quantity.
If we put x = 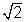 , x2 - 3 = - 1 but is + ve quantity so, we put - ve to make it + ve.
, x2 - 3 = - 1 but is + ve quantity so, we put - ve to make it + ve.
So, y = |x2 - 3| = - (x2 - 3)

Q.6. If ax2 + bx + c = 0, a,b,c 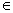 R. Find condition that this eq. would have at least one root in (0, 1).
R. Find condition that this eq. would have at least one root in (0, 1).
Ans: Let f’(x) = ax2 + bx + c
Integrating both sides, f(x) =
f(x) = 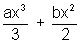 + cx + d ………………………………….. (i)
+ cx + d ………………………………….. (i) f(0) = d & f(1) =
f(0) = d & f(1) = 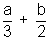 + c + d
+ c + d
Since, Rolle’s theorem is applicable.
[Dumb Question: Why Rolle’s theorem is applicable ?
Ans: Rolle’s theorem is applicable b/c f(x) is polynomial function which is continuous & differentiable everywhare.] f(0) = f(1)
f(0) = f(1)
 2a + 3b + 6c = 0 2a + 3b + 6c = 0 |
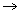 required condition.
required condition.Q.7. Let f(x) & g(x) be differentiable for 0
 x
x 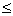 2 such that f(0) = 2, g(0) = 1 & f(2) = 8. Let there exists a real no. c in [0, 2] such that f'(c) = 3g'(c) find value of g(2).
2 such that f(0) = 2, g(0) = 1 & f(2) = 8. Let there exists a real no. c in [0, 2] such that f'(c) = 3g'(c) find value of g(2).Ans: As f(x) & g(x) are cobt. & differentiable in ... then there exists atleast one value 'c' such that
f'(c) =
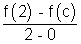
 g'(c) =
g'(c) = 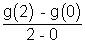
But
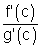 = 3
= 3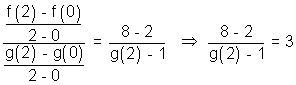
 g(2) = 3
g(2) = 3Q.8. f(x) is a polynomial of degree 4 with real coeff. such that f(x) = 0 is satisfied by x = 1, 2, 3 only, them and f'(1) f'(2) f'(3) ?
Ans: f(x) = 0 has only roots 1, 2, 3 only
But it is degree 4 eq.
 Any one of 1, 2, or 3 is 4 repeated root of f(x) = 0
Any one of 1, 2, or 3 is 4 repeated root of f(x) = 0 f'(1) or f'(2) or f'(3) any one of them must be zero.
f'(1) or f'(2) or f'(3) any one of them must be zero. f'(1) f'(2) f'(3) = 0
f'(1) f'(2) f'(3) = 0Q.9. Find interval for which f(x) = x - cosx is increasing or dectreasing.
Ans: f(x) = x - cosx
Differentiating w.r.t. x
f'(x) = 1 - sinx
we know
-1
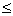 sinx
sinx 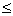 | for all x
| for all x 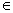 R
R....
 sin
sin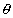
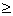 0 for x
0 for x Q.10. If a < 0, & f(x) = eax + e-ax is monotonically decreasing. Find interval to which x belongs.
Ans: Given a < o &
f(x) = eax + e-ax is decreasing
 f'(x) < 0
f'(x) < 0  aeax - ae-xx < 0
aeax - ae-xx < 0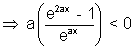
But a < 0
 (e2ax - 1) > 0
(e2ax - 1) > 0  e2ax > 1
e2ax > 1 2ax > 0
2ax > 0  ax > 1
ax > 1 x < 0 as a < 0
x < 0 as a < 0Medium Type:
Q.1. Find values of 'k' for which point min. of function f(x) = 1 + k2x - x3 satisfy inequality
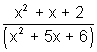 < 0.
< 0.Ans:
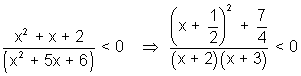
Since
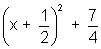 it always +ve
it always +ve (x + 2)(x + 3) < 0
(x + 2)(x + 3) < 0 - 3 < x < - 2 ........................................................ (i)
- 3 < x < - 2 ........................................................ (i)f(x) = 1 + k2x - x3
f'(x) = k2 - 3x2
f''(x) = - 6x
For max/min, f(x) = 0
 x = ±
x = ±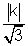
Let x1 =
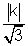 & x2 = -
& x2 = - 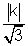
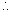 f''(x1) < 0 & f''(x2) > 0
f''(x1) < 0 & f''(x2) > 0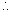 f(x) is max. at x = x1 & min. at x = x2
f(x) is max. at x = x1 & min. at x = x2But x2 is min. which lies b/w
- 3 < x2 < - 2 (from relation (i))
 - 3 < -
- 3 < - 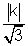 < - 2
< - 2 3
3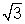 > |k| > 2
> |k| > 2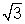
 k
k 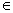 (- 3
(- 3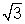 , - 2
, - 2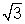 ) U (2
) U (2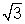 , 3
, 3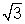 )
)Q.2. If f(x) =
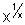 , x > 0 determine bigger of two no.
, x > 0 determine bigger of two no. 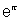 &
& 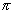 e.
e.Ans. y = f(x) =
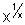 , x > 0
, x > 0Taking log on both sides
ln y =
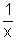 ln x
ln xDifferentiating both side
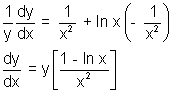
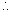 f'(x) =
f'(x) = 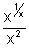 [1 - ln x]
[1 - ln x]Let f'(x) = 0
 log x = 0 or x = e
log x = 0 or x = ef''(x) =
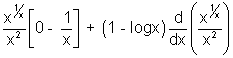
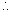 f''(e) =
f''(e) = 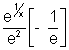 + 0
+ 0 f''(e) < 0
f''(e) < 0 f(x) has maxima at x = e
f(x) has maxima at x = e f(e) > f(
f(e) > f(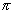 ) for all x > 0
) for all x > 0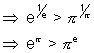
Q.3. If f(x) = ax3 + bx2 + cx + d where a, b, c, d are real no.s & 3b2 < c2, is an increasing cubic function & g(x) = af'(x) + bf''(x) + c2, then prove that
 is an increasing function.
is an increasing function.Ans: f(x) = ax3 + bx2 + cx + d
f'(x) = 3ax2 + 2bx + c
Since f(x) is increasing
f'(x) > 0
 3ax2 + 2bx + c > 0
3ax2 + 2bx + c > 0 3a > 0 & D < 0
3a > 0 & D < 0 3a > 0 & b2 - 3ac < 0
3a > 0 & b2 - 3ac < 0 a > 0 & b2 < 3ac ........................................ (i)
a > 0 & b2 < 3ac ........................................ (i)g(x) = af'(x) + bf''(x) + c2
g(x) = 3a2x2 + 2abx + ac + 6abx + 2b2 + c2
g(x) = 3a2x2 + 8abx + (2b2 + c2 + ac)
D = 64a2b2 - 4.3a2(2b2 + c2 + ac)
= 4a2(10b2 - 3c2 - 3ac)
Since 3ac > b2 from (i)
 - 3ac < - b2
- 3ac < - b2 4a2(10b2 - 3c2 - 3ac) < 4a2(10b2 - 3c2 - b2)
4a2(10b2 - 3c2 - 3ac) < 4a2(10b2 - 3c2 - b2)= 4a2(9b2 - 3c2)
Since 3b2 < c2
= 12a2(3b2 - c2) = -ve
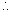 D < 0
D < 0 g(x) > 0
g(x) > 0 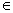 R
R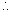
 is increasing function.
is increasing function.