Atomic - Structure-4
In case of a photon, if it is assumed to have wave character, its energy is given by
E = h
...(i)
de Broglie pointed out that the above equation is applicable to any material particle. The mass of the photon is replaced by the mass of the material particle and the velocity c of the photon is replaced by the velocity n of the material particle. Thus, for any material particle like electron, we may write
Distinction between a particle and a wave. The concept of a particle and a wave can be under-stood by the different points of distinction between them given in table 1.
Table Points of distinction between a particle and a wave
| Particle | Wave |
|---|---|
| 1. A particle occupies a well-defined position in space i.e. a particle is localized in space e.g. a grain of sand, a cricket ball etc. | 1. A wave is spread out in space e.g. on throwing a stone in a pond of water, the waves start moving out in the form of concentric circles. Similarly, the sound of the speaker reaches everybody in the audience. Thus a wave is delocalized in space. |
| 2. When a particular space is occupied by one particle, the same space cannot be occupied simultaneously by any other particle. In other words, particles do not interfere. | 2. Two or more waves can coexist in the same region of space and hence interfere. |
| 3. When a number of particles are present in a given region of space, their total value is equal to their sum i.e. it is neither less nor more. | 3. When a number of waves are present in a given region of space, due to interference, the resultant wave can be larger or smaller than the individual waves i.e. interference may be constructive or destructive. |
Characteristics of Matter waves and Electromagnetic waves. Matter waves differ from electromagnetic waves in the various respects given in table 2 on next page.
Significance of de Broglie equation. Although the de Broglie equation is applicable to all material objects but it has significance only in case of micro-scopic particles. This will be clear from the following example :
| Electromagnetic Waves | Matter Waves |
|---|---|
| 1. The electromagnetic waves are associated with electric and magnetic fields, perpendicular to each other and to the direction of propagation. | 1. Matter waves are not associated with electric and magnetic fields. |
| 2. They do not require any medium for propagation i.e. they can pass through vacuum. | 2. They require medium for their propagation i.e. they cannot pass through vacuum. |
| 3. They travel with the same speed as that of light. | 3. The speed of these waves is not the same as that of light. Moreover it is not constant for all matter waves. |
| 4. They leave the source. | 4. They do not leave the moving objects. |
5. Their wavelength is given by  = c/ |
5. Their wavelength is given by l = h/m |
Consider a ball of mass 0.1 kg moving with a speed of 60 m s-1. From de Broglie equation, the wavelength of the associated wave is 
or approx. 10-34 m. It is apparent that this wavelength is too small for ordinary observation. On the other hand, an electron with a rest mass equal to 9.11 × 10-31 kg i.e. approx. 10-30 kg moving at the same speed would have a wavelength 
m i.e. 105 Ã… which can be easily measured experimentally.
Since we come across macroscopic objects in our everyday life, therefore de Broglie relationship has no significance in everyday life. That is why we do not observe any wave nature associated with the motion of a running car or a cricket ball etc.
Experimental verification of the dual character of electrons.
(a) Verification of wave character.
(i)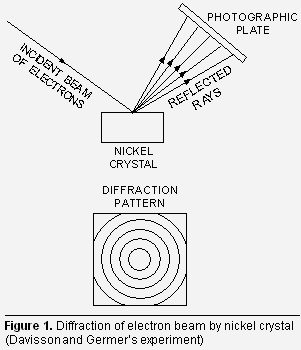 
Davisson and Germer’s experiment. Davisson and Germer in 1927 observed that when a beam of electrons is allowed to fall on the surface of a nickel crystal and the scattered or the reflected rays are received on a photographic plate, a diffraction pattern (consisting of a number of concentric rings), similar to that produced by X-rays, is obtained (Fig.1). Now, since X-rays are electromagnetic waves i.e., they are confirmed to have wave character, therefore, electrons must also have wave character. Moreover, the wavelength determined from the diffraction is found to be very nearly the same as calculated from de Broglie equation. This furhter lent support to de Broglie equation.
(ii)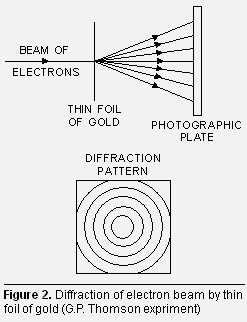
Thomson’s experiment. G.P. Thomson in 1928 performed experiments with thin foil of gold in place of nickel crystal. He observed that if the beam of electrons after passing through the thin foil of gold is received on the photographic plate placed perpendicular to the direction of the beam, a diffraction pattern is observed as before (Fig. 1). This again confirmed the wave nature of electrons.
(b) Verification of the particle character. The particle character of the electron is proved by the following different experiments :–
(i) When an electron strikes a zinc sulphide screen, a spot of light known as scintillation is produced. Since a scintillation is localized on the zinc sulphide screen, therefore the striking electron which produces it also must be localized and is not spread out on the screen. But the localized character is possessed by particles (as already explained on page below). Hence electron has particle character.
(ii) Experiments such as Thomson’s experiment for determination of the ratio of charge to mass (i.e. e/m) and Milliken oil drop experiment for determination of charge on electron also show that electron has particle character.
(iii) The phenomenon of Black body radiation and Photoelectric effect also prove the particle nature of radiation.
The most important application of de Broglie concept is in the construction of electron microscope which is used in the measurement of size of very small objects.
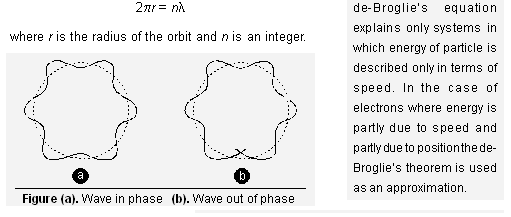
Derivation of Bohr’s postulate of angular momentum from de Broglie equation. According to Bohr’s model, the electron revolves around the nucleus in circular orbits. According to de Broglie concept, the electron is not only a particle but has a wave character. Thus in order that the wave may be completely in phase (Fig. (a), the circumference of the orbit must be equal to an integral multiple of wavelength () i.e.,
Heisenberg’s Uncertainty Principle
All moving objects that we see around us e.g. a car, a planet, a ball thrown in the air etc move along definite paths or trajectories. Hence their position and velocity can be measured accurately at any instant of time. However, such an accurate measurement is not possible for sub-atomic particles.
As a consequence of dual nature of matter, Werner Heisenberg, a German physicist, in 1927 gave a principle about the uncertainties in simultaneous measurements of position and momentum of small particles. It is known as Heisenberg’s uncertainty principle and it states as follows :
It is impossible to measure simultaneously the position and momentum of a small particle with absolute accuracy or certainty. If an attempt is made to measure any one of these two quantities with higher accuracy, the other becomes less accurate. The product of the uncertainty in the position (
x) and the uncertainty in the momentum (p = m. where m is the mass of the particle and is the uncertainty in velocity) is always constant and is equal to or greater than h/4
x . p>=h/4 ...(i)However, for most of the purposes (e.g. in the numerical problems), the mathematical expression for the Heisenberg’s uncertaintly principle is simply written as
...(ii)Keeping in view the expression (i), the value of
p calculated for a given value of x using the expression (ii) is the minimum value for p. Similarly, the value of x calculated for a given value of p will be the minimum value for x.Explanation
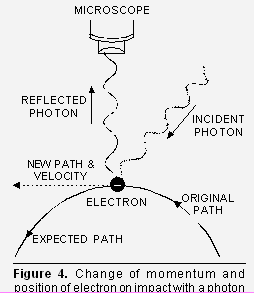of Heisenberg’s uncertainty principle. The basis for the above principle may be understood from the following description :Suppose we attempt to measure both the position and momentum of an electron. To pin-point the position of the electron, we have to use light so that the photon of light strikes the electron and the reflected photon is seen in the microscope (Fig. 4). As a result of the hitting, the position as well as the velocity of the electron are disturbed.
But according to principle of optics, the accuracy with which the position of a particle can be measured depends upon the wavelength of light used. The uncertaintly in position is ±. The shorter the wavelength, the greater is the accuracy. But shorter wavelength means higher frequency and hence higher energy. This high energy photon on striking the electron changes its speed as well as direction.
Alternatively, shorter wavelength implies higher momentum (as = h/p i.e. p = h/). Thus photon will have higher momentum and a larger but indefinite amount of it will be transferred to the electron at the time of collision. This will result in greater uncertainty in the velocity of the electron. On the other hand, decreasing the momentum means increasing the wavelength which will lead to greater uncertainty in position.
Significance of Heisenberg’s uncertainty principle. Like de Broglie equation, although Heisenberg’s uncertainty principle holds good for all objects but it is of significance only for microscopic particles. The reason for this is quite obvious. The energy of the photon is insufficient to change the position an velocity of bigger bodies when it collides with them. For example, the light from a torch falling on a running rat in a dark room neither changes the speed of the rat nor its direction i.e. position. Since in everyday life, we come across big objects only, the position and velocity of which can be measured accurately, Heisenberg’s uncertainty principle has no significance in everyday life.
Why electron cannot exist in the nucleus? On the basis of Heisenberg’s uncertainty principle, it can be shown why electrons cannot exist within the atomic nucleus. This is because the diameter of the atomic nucleus is of the order of
10-14 m. Hence if the dlectron were to exist within the nucleus, the maximum uncertainty in its position would have been
10-14 m. Taking the mass of electron as 9.1 × 10-31 kg, the minimum uncertainty in velocity can be calculated by applying uncertainty principle as follows:–
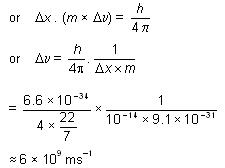
This value is much higher than the velocity of light (viz 3 × 108 ms--1) and hence is not possible.
BLACK BODY RADIATION AND PHOTOELECTRI EFFECT
Black body radiation. If any substance with high melting point (e.g, an iron bar) is heated, it first becomes red, then yellow and finally begins to glow with white light.
If the substance beings heated is a black body (which is a perfect absorber and perfect radiator of energy) the radiation emitted is called black body radiation.
According to electromagnetic wave theory, the energy is emitted or absorbed continuously. Hence, the energy of any electromagnetic radiation is proportional to its intensity i.e. a square of amplitude and is independent of its frequency or wavelength. Thus, according to the wave theory, the radiation emitted by the body being heated should have the same colour, although its intensity may vary as the heating is continued.
Photoelectric effect. When radiations with certain minimum frequency (
) strike the surface of a metal, the electrons are ejected from the surface of the metal (Figure). This phenomenon is called photoelectric effect. The electrons emitted are called photo-electrons.
However, the following three important facts are obwerved about the photoelectric effect :
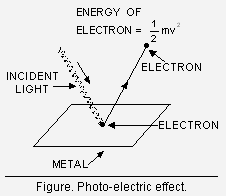
(i) The electrons are ejected only if the radiation striking the surface of the metal has at least a minimum frequency (). If the frequency is less than , electrons are ejected. This value () is called Threshold Frequency.
(ii) The velocity (and hence the kinetic energy) of the electron ejected depends upon the frequency of the incident radiation and is independent of its intensity.
(iii) The number of photoelectrons ejected is proportional to the intensity of incident radiation.
The above observations cannot be explained by the Electromagnetic wave theory. According to this theory, since radiations are continuous, therefore it should be possible to accumulate energy on the surface of the metal, irrespective of its frequency and thus radiations of all frequencies should be able to eject electrons.
Similarly, according to this theory, the energy of the electrons ejected should depend upon the intensity of the incident radiation.
2. Planck’s Quantum Theory. To explain the phenomena of ‘Black body radiation’ and ‘Photoelectric effect,’ Max Planck is 1900, put forward a theory known after his name as Planck’s quantum theory. This theory was further extended by Einstein in 1905. The main points of this theory are as follows:—
(i) The radiant energy is emitted or absorbed not continuously but discontinuously in the form of small discrete packets of energy, Each such packet of energy is called a ‘quantum’. In case of light, the quantum of energy is called a ‘photon’.
(ii) The energy of each quantum is directly proportional to the frequency of the radiation,* i.e.,
where h is a proportionality constant, called Planck’s constant. Its value is approx. 6.62 × 10-27 erg. sec. or
6.62 × 10-34 joules sec.
(iii) The total amount of energy emitted or absorbed by a body will be some whole number quanta. Hence 
where n is any integer.