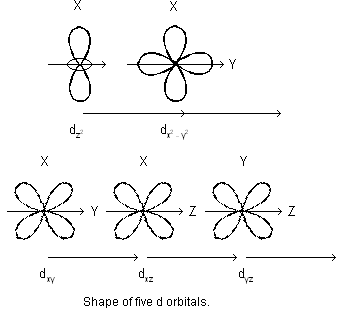Atomic - Structure-5

Explanation of Black body radiation and Photoelectric effect.

Explanation of Black Body Radiation. When some solid substance is heated, the atoms of the substance are set into oscillation and emit radiation of frequency, . Now, as heating is continued, more and more energy is being absorbed by the atoms and they emit radiations of higher and higher frequency. As red light has minimum frequency, yellow has higher frequency, therefore, the body on heating becomes first red, then yellow and so on.

Explanation of Photoelectric effect. Planck’s quantum theory gives an explanation of the different points of the photoelectric effect as under :
(i) When light of some particular frequency falls on the surface of metal, the photon gives its entire energy to the electron of the metal atom. The electron will be dislodged or detached from the metal atom only if the energy of the photon is sufficient to overcome the force of attraction of the electron by the nucleus. That is why photo-electrons are ejected only when the incident light has a certain minimum frequency (threshold frequency ).
(ii) If the frequency of the incident light () is more than the threshold frequency (), the excess energy is imparted to the electron as kinetic energy. i.e. K.E. of the ejected electron =. Hence greater is the frequency of the incident light, greater is the kinetic energy of the emitted electron**.
(iii) Increasing the intensity of light of a given frequency increases the number of photons but does not increase the energies of photons. Hence, when the intensity of light is increased, more electrons are ejected but the energies of these electrons are not altered.

*Thus, in the visible light, as violet radiations have maximum frequency and the red radiations have minimum frequency violet light has more energy than the red light. Similarly, the ultraviolet light has higher energy than the violet light and the infrared light has less energy than even the red light.

**If 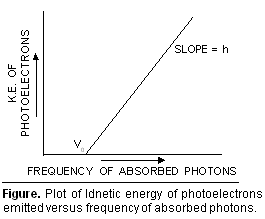kinetic energy of the emitted photo-electrons is plotted against the frequency of the absorbed photons, a straight line of slope h is obtained (Figure).
Stopping potential ; The minimum potential at which the plate photoelectric current becomes zero is called stopping potential. If is the stopping potential, then

 

 

Theories of Nuclear Stability
Since a nucleus contains positively charged protons, there must exist a strong repulsive force between them. It has been calculated that there exists an electrostatic repulsion of approximately six tons between two protons situated at a nuclear distance but at the same time the forces which bind the nucleus are very high. It has been found that nuclear forces attracting the same two particles (i.e., protons) are at least forty times greater than the repuslive forces. Thus, two major forces exist in the nucleus. These are electrostatic and nuclear. The nuclear forces are stronger and the range of these forces is extremely small. The forces which operate between nucleons are referred to as exchange forces. In order to account for the stability of the nucleus, a theory known as meson theory was put forward by Yukawa, in 1935. Yukawa pointed out that neutrons and protons are held together by very rapid exchange of nuclear particles called pi mesons. These mesons may be electrically neutral, positive or negative (designated as ,, ) and possess a mass 275 times the mass of an electron. Nuclear forces arise from a constant exchange of mesons between nucleons with very high velocity (practically the velocity of light).
Let a neutron be converted into a proton by the emission of a negative meson. The emitted meson is accepted by another proton and converted into a neutron.

Similarly, a proton after emitting a positive meson is converted into a neutron and vice-versa.

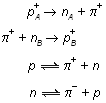
There may be two more types of exchange, i.e., between neutron-neutron and proton-proton, involving neutral pi mesons.

Mass defect—Binding energy
It is observed that the atomic mass of all nuclei (except hydrogen) is different from the sum of the masses of protons and neutrons. For example, the helium nucleus consists of 2 protons and 2 neutrons. The combined mass of 2 protons and 2 neutrons should be

The actual observed mass of helium nuclei is 4.0028 amu. A difference of 0.0302 amu is observed between these two values. This difference is termed as mass defect.

This decrease in mass (i.e., mass defect) is converted into energy according to Einstein equation E = mc². The energy released when a nucleus is formed from protons and neutrons is called the binding energy. This is the force which holds all the nucleons together in the nucleus. Binding energy can be defined in other ways also, i.e., the energy required to break the nucleus into constituent protons and neutrons. Binding energy is measured in MeV (million electron-volts), i.e., 1 amu = 931 MeV.

Binding energy can also be calculated in ergs. This is:

The binding energy increases with the increase in atomic number of the element. This indicates that heavier nuclei should be more stable than lighter nuclei. But, it is not so because heavier nuclei above atomic number 82 are unstable. It is thus clear that total binding energy of a nucleus does not explain the stability of the nucleus.

The total binding energy of a nucleus when divided by the number of nucleons gives the average or mean binding energy per nucleon. The binding energy per nucleon is actually the measure of the stability of the nucleus. The greater the binding energy per nucleon, more stable is the nucleus.

When binding energy per nucleon of a number of nuclei is plotted against the corresponding mass number, a graph is obtained (Figure) whose characteristics are as follows:

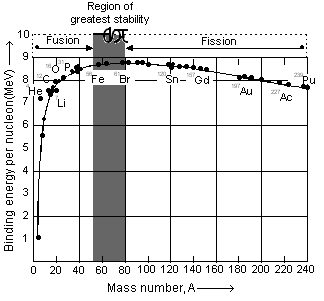
(i) Binding energy per nucleon increases from 1.1 to 8.0 MeV from mass number 2 to 20.
(ii) Binding energy per nucleon increses from 8 to 8.6 MeV from mass number 20 to 40.
(iii) Binding energy per nucleon remains 8.6 – 8.7 MeV from mass number 40 to 90. Iron (56) has the maximum value of 8.7 MeV per nucleon.
(iv) The value of binding energy per nucleon decreases from 8.6 to 7.5 MeV from mass number 90 to 240.
(v) Points for helium, carbon, oxygen lie quite high in the graph showing that these nuclei are highly stable.

The binding energy per nucleon can be increased in two ways:
(i) Either by breaking heavy nucleus to those of intermediate mass numbers (process of fission) or
(ii) By fusing lighter nuclei to form heavier nuclei (process of fusion).

Quantum Numbers
An atom contains a large number of orbitals. These are distinguished from each other on the basis of their size, shape and orientation (direction) in space. These parameters of an orbital are expressed in terms of three numbers, called principal, azimuthal and magnetic quantum numbers. Further to represent the spin (rotation) of the electron about its own axis, a fourth quantum number, called spin quantum number is introduced. Thus:

These numbers are like the postal address of a person. To know about a particular person, Mr X, we should know about his country, his town, his lane and house number.

The various quantum numbers are briefly described below :
1. Principal Quantum Number. It is represented by ‘n’. It gives the following information :
(i) Approximate distance of the electron from the nucleus i.e. the size of the electron cloud.
(ii) Energy of the electron present in any shell*, e.g. for hydrogen atom,
(iii) Maximum number of electrons present in any shell (given by the formula 2n2).
This number helps to explain the main lines of the spectrum.
It can have values n = 1, 2, 3, 4........etc. which are called K, L, M, N.......etc. shells respectively.

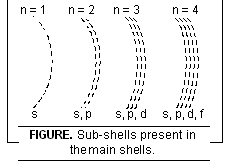
2. Azimuthal (or Subsidiary or Angular momentum) Quantum Number. This number is represented by ‘l’. It is found that the energy of an electron calculated from the value of n includes in itself some contribution due to angular momentum of the electron. As different electrons may have different angular momenta, the electrons within the same shell occupy different energy levels called sub-levels or sub-shells. The azimuthal quantum number gives the following information:
(i) Number of sub-shells present within any main shell
(ii) Contribution of energy due to angular momentum towards the total energy of the electron.
(iii) Relative energies of the sub-shells belonging to the same shell.
(iv) Shapes of the subshells.
(v) Orbital angular momentum which is equal to

This number helps to explain the fine lines of the spectrum because due to the presence of a large number of sub-levels, the number of probable transitions (jumps) of electrons becomes very large.

For a given value of n, l can have values from 0 to n – 1. For example,

For n = 1, l = 0 i.e. only one value
For n = 2, l = 0, 1 i.e. two values
For n = 3, l = 0, 1, 2, i.e. four values
For n = 4, l = 0, 1, 2, 3, i.e. four values
Thus 1st, 2nd, 3rd, 4th shells have 1, 2, 3, and 4 sub-shells respectively. In general, nth shell has n sub-shells.
Further, these sub-shells are designated by the letters s, p, d and f for l = 0, 1, 2, and 3 respectively (derived from the first letter of the words sharp, principal, diffused and fundamental lines of the spectra)

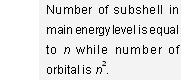
Shell	Sub-shells present
1st (K)	1s
2nd (L)	2s, 2p
3rd (M)	3s, 3p, 3d
4th (N)	4s, 4p, 4d, 4f

(The prefix before the symbol of sub-shell represents value of n)

The number of sub-shells within the various main shells are shown in Fig. below.

The energies of the different sub-shells present within the same main shell are found to be in the order s < p < d < f

Further the electron cloud of ‘s’ is found to be spherical while that of ‘p’ is found to be dumb-bell shaped. d and f have complex shapes.

3. Magnetic Quantum Number. This number is represented by ‘m’. This number is required to explain the fact that when the source giving the line spectrum is placed in a magnetic field, each spectral line splits into a number of lines (Zeeman effect). This was obviously due to the fact that each subshell contains a number of orbitals which take up different orientations under the influence of the external magnetic field. The magnetic quantum number tells the number of orientations which the orbitals present within the same sub-shell can take up. In other words, it tells the number of orbitals present within the same sub-shell (as each orientation represents an orbital).

For a given value of l, m can have values from – l to + l including ‘0’. Thus

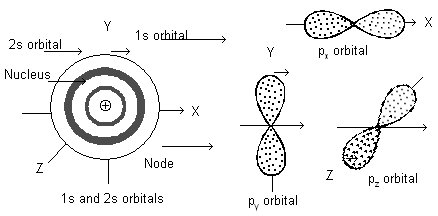
For s-sub-shell, l = 1. Hence m = – 1, 0, + 1 (three values) i.e. p-sub-shell has three orbitals oriented along X-axis, Y-axis and Z-axis and represented by p_x, p_y and p_z respectively*.

Similarly, for d-sub-shell, l = 2 so that m = – 2, – 1, 0, +1, +2 i.e. d-sub-shells contain five orbitals. For f-sub-shell, l = 3 so that m = – 3, – 2, – 1, 0, + 1, + 2, + 3 i.e. f-sub-shell has seven orbitals.

Different values of ‘m’ for a given value of ‘ l’ provide the total number of ways in which a given s,p,d,fsubshell in presence of magnetic field can be arranged in space along x,yand z axes or total number of orbitals into which a given subshell can be divided.