Atomic - Structure-6

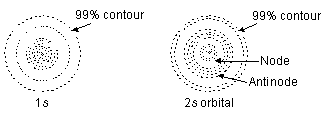
When l = 0, m = 0, i.e., one value implies that ‘s’ subshell has only one space orientation and hence, it can be arranged in space only in one way along x, yor z axes. Thus, ‘s’ orbital has a symmetrical spherical shape and is usually represented as in Figure below.

In case of 1s orbital the electron cloud is maximum at the nucleus and decreases with the distance. The electron density at a particular distance is uniform in all directions. The region of maximum electron density is called antinode. In case of ‘2s’ orbital, the electron density is again maximum at the nucleus and decreases with increase in distance. The ‘2s’ orbital differs in detail from a 1s orbital. The electron in a ‘2s’ orbital is likely to be found in two regions, one near the cucleus and other in a spherical shell about the nucleus. Electron density is zero in nodal region

When l = 1, ‘m’ has three values –1, 0, + 1. It implies that ‘p’ subshell of any energy shell has three space orientations, i.e., three orbitals. Each p-orbital has dumb-bell shape. Each one is disposed symmetrically along one of the three axes as shown in figure below. p-orbitals have directional character.

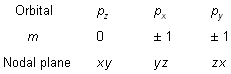
When l = 2, ‘m’ has five values –2, –1, 0, + 1, + 2. It implies that d-subshell of any energy shell has five orientations, i.e., five orbitals. All the five orbitals are not identical in shape. Four of the d-orbitals d_xy, d_yz, d_zx, contain four lobes

while fifth orbital consists of only two lobes. The lobes of orbital lie between x and y axes. Similar is the case for and . Four lobes of orbital are lying along x and y axes while the two lobes of orbital are lying along z axes and contain a ring of negative charge surrounding the nucleus in xy plane figure below.

Orbital
m	± 2	± 1	± 1	± 2	0

There are seven f-orbitals designated as Their shapes are complicated ones.

Spherical nodes and nodal planes
(a) Spherical node. The spherical surface where the probability of finding an electron is zero is called a spherical node.
In general, number of spherical nodes in an orbital = n – l – 1.
where n is the principal quantum number and l is the azimuthal quantum number. For example,

(i)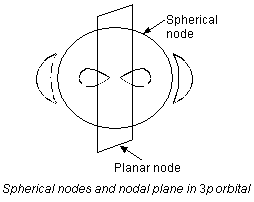 For 1s, n = 1 and l = 0
No. of spherical nodes = 1 – 0 – 1 = 0

(ii) For 2s, n = 2 and l = 0
No. of spherical nodes = 2 – 0 – 1 = 1

(iii) For 2p, n = 2 and l = 1
No. of spherical nodes = 2 – 1 – 1 = 0

(iv) For 3s, n = 3 and l = 0
No. of spherical nodes = 3 – 0 – 1 = 2

(iv) For 3p, n = 3 and l = 1
No. of spherical nodes = 3 – 1 – 1 = 1

b) Nodal planes. The planes in which the probability of finding an electron is zero is called a nodal plane. Number of nodal planes for an orbital = l. For example, (i) s-orbital (l = 0) has no nodal plane (ii) p-orbital (l = 1) has one nodal plane (iii) d-orbital (l = 2) has two nodal planes (iv) f-orbital (l = 3) has three nodal planes.
1. The designation of the seven f-orbitals are .
2. In the plots of radial probability versus distance from nucleus, number of peaks i.e. regions of maximum probability = n – l (No. of radial nodes = n – l – 1 as already explained in the text).
3. 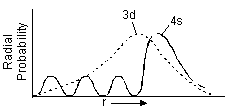The reason why 4s orbital has lesser energy than 3d orbital is that 4s-orbital has three small peaks closer to the nucleus (in addition to the 4th high peak). Thus 4s is more penetrating than 3d i.e. held more tightly to the nucleus and hence has lower energy.
4. The opposite lobes of p-orbitals have different signs (one +ve, the other –ve) but opposite lobes of d-orbitals have the same sign (two lobes have +ve sign while the other two have –ve sign).

4. Spin Quantum Number. It is represented by ‘s’. This number was introduced to account for the fact that the electron in an atom not only moves around the nucleus but also spins about its own axis (like the earth which not only revolves around the sun but also spins around its own axis). This number gives the information about the direction of spin-ning of the electron present in any orbital. Since the electron in an orbital can spin either in the clock-wise direction or in the anti-clockwise direction, hence for a given value of m, s can have only two values i.e. + 1/2 and – 1/2 or these are very often represented by two arrows pointing in the opposite direction i.e.

This quantum number helps to explain the magnetic properties of the substances. A spinning electron behaves like a micromagnet with a definite magnetic moment. If an orbital contains two electrons, the two magnetic moments oppose and cancel each other.

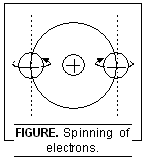
Thus in an atom, if all the orbitals are fully filled, net magnetic moment is zero and the sub-stance is diamagnetic (i.e. repelled by the external magnetic field). However, if some half-filled orbitals are present, the substance has a net magnetic moment and is paramagnetic (i.e. attracted by the external magnetic field).

Filling Of Orbitals Atoms
The filling of electrons into the orbitals of different atoms takes place according to the following three rules :
(1) Aufbau Principle. The word ‘aufbau’ in German means ‘building up’. The building up of orbitals means the filling up of orbitals with electrons. The principle states as follows :

In the ground state of the atoms, the orbitals are filled in order of their increasing energies. In other words, electrons first occupy the lowest-energy orbital available to them and enter into higher energy orbitals only when the lower energy orbitals are filled.

The order in which the energies of the orbitals increase and hence the order in which the orbitals are filled is as follows:

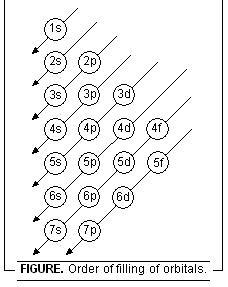
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p.....

This order may be remembered by using the method given in Figure below. Starting from the top, the direction of the arrows gives the order of filling of orbitals.
Alternatively, the order of increase of energy of orbitals can be calculated from (n + l) rule, explained in the next column.

The energy of an orbitals depends upon the values of principal quantum number, n and the azimuthal quantum number l (in the absence of an external magnetic field). The (n + l) rule states as follows :

Lower the value of (n + l) for an orbital, the lower is its energy. Hence orbitals are filled in order of increasing (n + l) values. If two orbitals have the same (n + l) value, the orbital with lower value of n has lower energy and hence is filled first.

The following table illustrates the (n + l) rule:


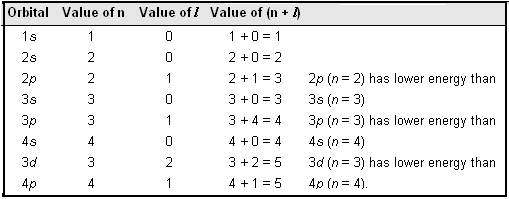
It may be noted that different subshells of a particular shell have different energies only in case of multi-electron atoms.

(2) Pauli Exclusion Principle. As already explained, Pauli exclusion principle states as follows:

An orbital can have maximum two electrons and these must have opposite spins.

If an orbital is represented by a circle and it contains two electrons, it is represented as:

i.e. the two arrows must point in the opposite direction. The electrons are said to be paired or the orbitals is said to be fully filled. It will be wrong to represent it as

If an orbitals contains only one electron, it is represented as

and is said to be half-filled. The electron is said to be in an unpaired state.

(3) Hund’s Rule of Maximum Multiplicity. This rule deals with the filling of electrons into the orbitals belonging to the same sub-shell (i.e. orbitals of equal energy, called degenerate orbitals). It states as under :

The pairing of electrons in the orbitals belonging to the same sub-shell (p, d or f) does not take place until each orbital belonging to that sub-shell has got one electron each i.e. is singly occupied.

Since there are three p, five d and seven f orbitals, therefore the pairing of electrons will start in the p, d and f orbitals with the entry of 4th, 6th and 8th electron respectively.

Since there are three p, five d and seven f orbitals, therefore the pairing of electrons will start in the p, d and f orbitals with the entry of 4th, 6th and 8th electron respectively.

The reason for such a tendency in quite obvious. The electrons are negatively charged and repel each other. Hence they spread out and occupy the identical orbitals singly before they begin to pair. As a result, the repulsions are minimum. Hence the energy is minimum and the stability is maximum. Pairing occurs because less energy is needed to do so than the energy required to place the electron in the next higher empty orbital.

Further it is important to note that whenever orbitals are singly occupied as above, the electrons present in them have the spin in the same direction i.e. either all clockwise or all anticlockwise. This is because of the fact that such a state has lower energy and hence is more stable.

Electronic Configuration of Atoms

The distribution of electrons into different levels, sublevels and orbitals of an atom is called its electronic configuration

Keeping in view the above rules, and representing an orbital by a circle and an electron and the direction of its spin by an arrow, the electronic configurations of the first 12 elements may be represented as follows :