Atomic Structure - 2

Calculation of radius of orbit:

Derivation:

Electrons revolves in orbit.

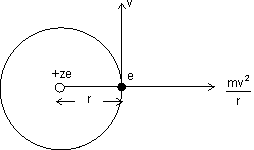
Centripetal force acting on electron away from centre & force of attraction towards centre.
For electron to revolve in same orbit.
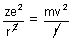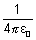           [ = 1 in CGS unit] ....................... (i)
       mvr = n 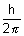....................................................... (ii)
       v =
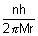
Putting value of v from eq. (ii) in eq. (i)
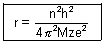       .................................................... (iii)
       r₀ = 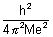= 0.529 A⁰ Bohr radius

For H-atom, rn = n2 x r0 = n2 x 0.529 A0

For H-like atom, like He⁺,


Calculation energy of electron:

Total energy of electron (E) = K.E. + P.E.
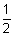                                       = mv² -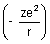


Dumb Question: Why P.E. is - ?

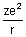Ans: P.E. is work done when electron moves from 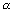to r.
       P.E. =


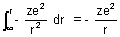
Dumb Question: Why Force is -ve ?

Ans: Force is work attractive. So, it is taken as -ve.
From eq. (i)   mv² =
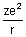
                   E = - = -


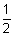
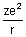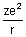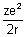
Dumb Question: What does -ve sign signify ?

Ans: -ve sign show's that electron is bound to that orbit & atom.
         E = -
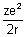
Substituting value of r from eq. (iii)
..................


Calculation of velocity of electron in any orbit:

Substituting value of r from (ii) in (i)
       v =
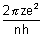
For H-like atom,
       v_n = 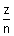x 2.188 x 10⁸ cms^-1
For H-atom, putting z = 1
       v_n = 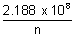cms^-1
From eq. (i)
       v² =
      


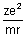
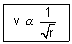
Calculation of no. of revolutions of electron in an orbit per sec:

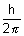
       mvr = n  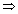 v =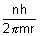
No. of rev./sec =
                    
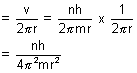
No. of revolutions per sec =
                                    =


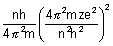
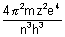
Calculation of no. of waves in any orbit:

No. of waves in any orbit =
                                   
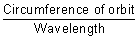
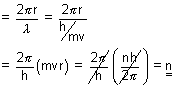
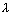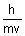
                                = De Broglie relation.

Waver no.: It is reciprocal of wavelength.
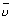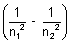For H-atom    (wave no.) = R       R 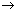Rydberg constant
                                                             R = 1.097 x 10⁷ m^-1
For Lyman Series n₁ = 1,    n₂ = 2, 3, 4, .....................................
For Balmer Series n₁ = 2,    n₂ = 3, 4, 5, .....................................
For Paschen Series n₁ = 3,    n₂ = 4, 5, 6, .....................................
For Brackett Series n₁ = 4,    n₂ = 5, 6, 7, .....................................
For Pfund Series n₁ = 5,    n₂ = 6, 7, 8, .....................................
For H-like atom,
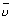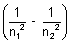                           = Rz²
                                z - atomic No.

when n₂ in Redbergis formula is 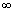i.e. n₂ =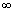


De Broglie Relation:

Matters have dual nature of particle & wave If assumed as wave, its energy.
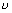
        E = h 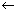Plank's quantum theory .................................... (i)
If assumed as particle, its energy.
        E = mc² 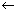Einstein Eq. .................................................. (ii)
Equating (1) & (2)
        h 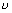= mc²
sinc   =
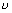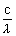
        h 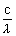= mc²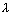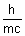
     

=

Deg broglie pointed that this eq. can be applicable to any particle.
         = =
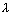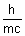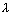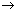         = de broglie wavelength.