Binomial Theoram is one chapter in which you see a question and then realise that it can easily be done in 2 or 3 ways. Definitely one of the most interesting chapters which uses concepts from calculus, trignometry, complex number prognessiong and wkhat not Binomial theoram finds use in number theory as well. So, let us prober deeper into this section.
Binomial theorm
Definition of Bionomial theoram
If n is a +ve integer and x
1 y are 2 complex number then .
(x + y)
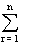n 
n C
r x
n-r y
r
=
nC
oX
n -
nC
1 X
n-1 y +
nC
2 X
n-2 y
2 +............+
n C
n y
n
Similarly (x - y)
n =
nC
oXn - nC1 Xn-1 y + nC2 Xn-2 y2 +.......+ (-1) n n Cn yn
The oefficients n Co, nC1, .................nCn are called Bionomial coeff.
Some important facts
(i) There are (n + 1) tevms in the expression .
(ii) lthe sum of in dices. Of x and y in each term of expansion is n .
(iii) The bionomial 3efficent of the terms equidistant from begining and the end are equal .
(iv) The r-th term from end in (x + y)n = (h + r + 2) th term from beginning .
General term.
In the expansion of (x + y)n the (r + 1tn) term from beginning of expansion is
Tr + 1 = nCr an-r bb
Illustration 1
Expand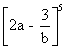 
by biobomial theoram .
Ans:- Using bionomial theoram we get
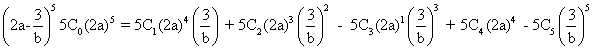
= 32 a5 -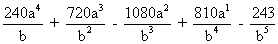 
Illustration 2.
If the ratio of 7th term from beginning to the seventh term from the end in the expassion of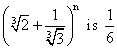 
then what is n .
Ans T7 from end of (a + b)n is same as T7 from beginning of (b + a)n
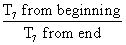of (a + b)n
or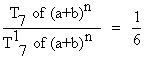 
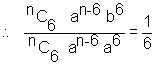
or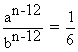 
or ( 2 1/3 3 1/3 ) n - 12 =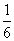 
=> 
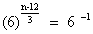
or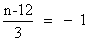 
So, n = 9