Greates Binomial coefficient(or Middle terms)(1) If n is even, then there is only one middle term which (h/2 + 1)
th term i.e.
T
n/2 + 1 =
n C
n/2 X
n/2and
nC
n/2 is greatest bionomial coefficient
(2) If n is each them trere are two middle terms which are
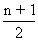th and
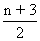th terms i.e
=
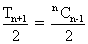
a
(n+1)/2 b
(n-1)/2and
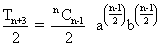
And,
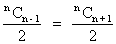
are greatest bionoimial ccoefficients
Numarically Greatest term of Bionmial expansion(a + x)
n = Co a
n + C
1 a
n-1 x.........+ C
n-1ax
n-1 + C
nx
n.
The numerically greatest term will be T
r+1 where r = ....
If
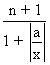
itself is a natural number then T
r = T
r+1both are numerically greatest terms.
Why ?
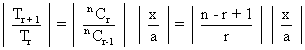
If
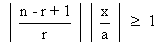
for given a, x and n
then
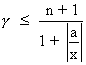
So, when
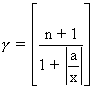Illustration 3Show that middle term in the expansion of (1 + x)
2n is img........... where n isa +ve integer.
Ans This number of terms in expassion of (1 + x)
2n is 2n + 1 (odd)
So, its middle term is (n + 1)
th term.
Required Term = T
n+1 =
2n C
n x
n=
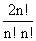
x
n=
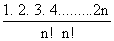
x
n=
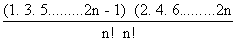
x
n.
=
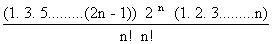
x
n=
=
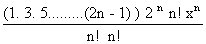
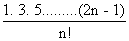
2
n x
nIllustration 4find the greatest term in the expansion of
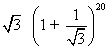Ans Let us find r =
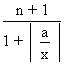
So, r =
=
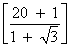
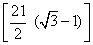
= 7
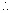
T
r+1 = T
8 is greatest term
Now T
8 =
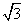20 C
7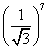
=
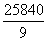Summation of series of Bionomial co-efficients.
Series of Bionomia cofficients cn be umme by uing methods like by taaking prouct o expnion of two bionomial by differentiating bionomial expansion, integraating bionomial expansion by equating real and imaginory part of a eries etc.
(1) Sum of sevies by taking product o expnsions of two bionomials if we find the product of binomial coefficients in tnhe sevies then this method can be used .