Binomial Theorem - 3
Illustration 5
Prove that C02 + C12 + C22+..............Cn2 =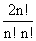
Ans : We know .
(1 + x)n = C0+ C1 C2 x2.......+Cn-1xn-1 + Cnxn
Also. (x + 1)n = C0 xn + C1 xn-1 + C2 xn-2+........... + Cn-1x + Cn
Now Let us multiply the two expansions and compare the coefficient of xn on both side .
(1 + x)n (x - 1)n = (C0 + C1 x + C2 x2 ........+Cnx + xn) X
(C0 xn + C1 xn-1 + C2 xn-2+........... + Cn-1x + Cn )
Coefficient of xn in (1 + n)n (1 + n)n
=> Coeff. of xn in (1 + x)2n
= 2nCn
Coeff. of xn in ( C0 + C1 x+ C2 x2 +......Cn xn ) X
(C0xn + C1xn + ..........+Cn)
= C02 + C1 2 + C22+............+ Cn-12 + Cn2
C02 + C1 2 + C22+............+ Cn-12 + Cn2
So, Comparing the coefficients un the 2 sidse we get .
C02 + C12 + C22+............+ Cn-12 + Cn2= 2n Cn
=
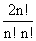
(2) Sum of sevies by use of differentiation:
When numericals occur as product of bionomial Coefficients this method is used .
Illustration 6
Find thesum of the following sevies.
C0 + 2C1 + 3C2 +...............+ (n + 1) Cn?
Ans We know that
(1 + x)n = C0 + C1x +C2 x2 + ..................+Cn xn
So, Multiplying both sides with x we get
x(1 + x)n = C0 x + C1 x2 + C2 x3 + ........+Cn x n+1
Now differentiating both sides with respect x we get
xn(1 + x)n-1 + (1 + x)n = C0 + 2C1x + 3c2 x2+...........+(n + 1) Cn xn
Now put x = 1
So, n 2n-1 + 2n = C0 + 2c1 + 3C2+...........+ (n + 1)Cn
So, C0 + 2c1 + 3C2+...........+(n + 1)Cn = (n + 2)2n-1
Dumb Question:- Why did we multiplied bionomial expansion with x imitially ?
Ans Observe taht the numreicals with bionomial coefficints were one more in value that the corresponding power of x, So we needed to multiply the expassion by x.
(3) Sum of series by use of integration
Whan nummericals occuv as the denominator of the bionomial Coefficient we apply this method .
Illustration 7.
Find the sum of series 2Co + 2 2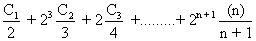
And
We know
(1 + x) n = C0 + C1 x + C2 x2 +..........+ Cnxn
Integrating both sides with respect to x we get
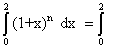(C0 + C1 x + C2 x2 +..........+ Cnxn) dx
=>
2Co + 22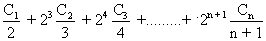
=
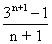
(4) Sum of the series by equation real and imaginary parts.
Somctimes the use of complex nos make the calculation very easy .
Prove that C02 + C12 + C22+..............Cn2 =
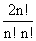
Ans : We know .
(1 + x)n = C0+ C1 C2 x2.......+Cn-1xn-1 + Cnxn
Also. (x + 1)n = C0 xn + C1 xn-1 + C2 xn-2+........... + Cn-1x + Cn
Now Let us multiply the two expansions and compare the coefficient of xn on both side .
(1 + x)n (x - 1)n = (C0 + C1 x + C2 x2 ........+Cnx + xn) X
(C0 xn + C1 xn-1 + C2 xn-2+........... + Cn-1x + Cn )
Coefficient of xn in (1 + n)n (1 + n)n
=> Coeff. of xn in (1 + x)2n
= 2nCn
Coeff. of xn in ( C0 + C1 x+ C2 x2 +......Cn xn ) X
(C0xn + C1xn + ..........+Cn)
= C02 + C1 2 + C22+............+ Cn-12 + Cn2
C02 + C1 2 + C22+............+ Cn-12 + Cn2
So, Comparing the coefficients un the 2 sidse we get .
C02 + C12 + C22+............+ Cn-12 + Cn2= 2n Cn
=
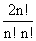
(2) Sum of sevies by use of differentiation:
When numericals occur as product of bionomial Coefficients this method is used .
Illustration 6
Find thesum of the following sevies.
C0 + 2C1 + 3C2 +...............+ (n + 1) Cn?
Ans We know that
(1 + x)n = C0 + C1x +C2 x2 + ..................+Cn xn
So, Multiplying both sides with x we get
x(1 + x)n = C0 x + C1 x2 + C2 x3 + ........+Cn x n+1
Now differentiating both sides with respect x we get
xn(1 + x)n-1 + (1 + x)n = C0 + 2C1x + 3c2 x2+...........+(n + 1) Cn xn
Now put x = 1
So, n 2n-1 + 2n = C0 + 2c1 + 3C2+...........+ (n + 1)Cn
So, C0 + 2c1 + 3C2+...........+(n + 1)Cn = (n + 2)2n-1
Dumb Question:- Why did we multiplied bionomial expansion with x imitially ?
Ans Observe taht the numreicals with bionomial coefficints were one more in value that the corresponding power of x, So we needed to multiply the expassion by x.
(3) Sum of series by use of integration
Whan nummericals occuv as the denominator of the bionomial Coefficient we apply this method .
Illustration 7.
Find the sum of series 2Co + 2 2
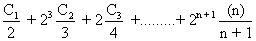
And
We know
(1 + x) n = C0 + C1 x + C2 x2 +..........+ Cnxn
Integrating both sides with respect to x we get
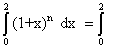(C0 + C1 x + C2 x2 +..........+ Cnxn) dx=>
2Co + 22
=
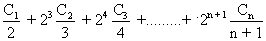
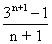
(4) Sum of the series by equation real and imaginary parts.
Somctimes the use of complex nos make the calculation very easy .