Binomial Theorem - 4
Illustration 8
If (3 + 4x)n = P0+ P1x + P2x2 +...+ Pnxn then prove that (Po - P2 + P4...)2 + (P1 - P3+ P5 ....)2 = 25n
Ans . Let us put x = i in the expansion
(3 + 4x)n = Po+ P1x + P2 x2 +.............+Pnxn
So, we get
(3 + 4i)n = (Po + P2 + P4 ...........) + i (P1 -P3 + P5 ...............)
Now equating the square of the modulus, we get
(Po + P2 + P4 ...........) 2+ (P1 -P3 + P5 ...............)2
= (32+ 42) n
= 25 n
Dumb Question Why did P4 got a +ve sign in front of it ?
Ans P4 is Coefficient of x4 . So,when we put i. i4 gives the sign and .
i4 = (i2)2 = (-1)2 = 1
Binomial Series (for negative or fractional indices)
If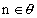
and | x | < 1, then
(1 + x)n = 1 + nx +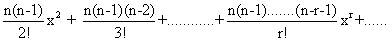
General term = T r+1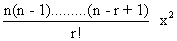
Illustration 9
Find the coefficients of x4andx-4 in expansion of
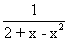, | < x < 2 .
=
=
=
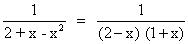
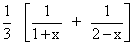
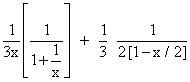
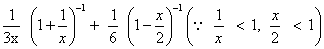
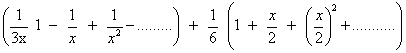
Coefficient of x4 = 0 +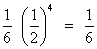
Coefficient of x-4 =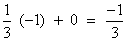
Binomial Theoram
If n is a positive integer then
( a1 + a2 + ........+ am) n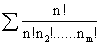
a1n1a2n2. a3n3.......am nm
Where the summation is taken over all non-negative integers n1, n2 ..........nm such that n1+ n2 + n3+.....+ nm = n
and the number of terms in the expansion is
= number of non-negative integral soln of equation
n1 + n2 +..........+nm
= n + m -1 Cm-1
Illustration 10 .
find the total number of terms in the kexpansion
of (x + y + z + w) n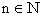
Ans. From Hultinomial Theorm
(x + y + z +w )n =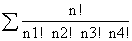
x1n1 y n2 zn3 wn4
where n1, n2, n3, n4 are non negative integers subject to the condition n1 + n2 + n3 + n4 = n
Hence no of distinct terms
= Coefficient of xnin (xo + x1 + x2 +.......+xn)4
= Coefficient of xn in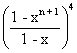
= Coefficient of x nin (1 - xn+1)4 (1 - x)-1
= Coefficient of x nin (1 - x)-4 (since xn+1
= n + 3Cn
=
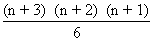
Dumb Question Why is no of disfinft terms equal to coefficient
of xn in (xo + x1 + x2+....................+xn )4 ?
Ans This is actually a problem of permutation and combipnation
But Let us discuss it here very brifly .
Equation is n1 + n2 + n3 + n4 = n
Now n1 can vary from o to n
Similar is the case for n2, n3 and n4.
So, xo + x1 + x2 +..................+ xn for n1
and (xo + x1 + x2 +..................+ x)4 for all n1, n2 + n3 and n4.
And then we try to find coeft of xn as n1 n2+ n3 + n4 head to sum to n
Easy
(1)Prove that Co + C1 + C2+..........Cn = 2n
Ans we know
Co + C1 + C2+..........Cnxn = (1 + x) n
Now put x = 1 or both sides
Co + C1 + C2+..........Cn = 2n
(2) find the sum kof series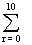
20 Cr ?
Ans We know =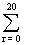
20 Cr = 220
Now L.H.S. mhas 21lterms out of which 10 pairs are equal.
because nCr= nCn - r
So, L.H.S. 2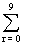
20 Cr - 20 C10 = 220
So, 2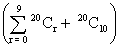
= 2 20 + 20 C10
or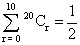
(2 20 + 20 C10)
If (3 + 4x)n = P0+ P1x + P2x2 +...+ Pnxn then prove that (Po - P2 + P4...)2 + (P1 - P3+ P5 ....)2 = 25n
Ans . Let us put x = i in the expansion
(3 + 4x)n = Po+ P1x + P2 x2 +.............+Pnxn
So, we get
(3 + 4i)n = (Po + P2 + P4 ...........) + i (P1 -P3 + P5 ...............)
Now equating the square of the modulus, we get
(Po + P2 + P4 ...........) 2+ (P1 -P3 + P5 ...............)2
= (32+ 42) n
= 25 n
Dumb Question Why did P4 got a +ve sign in front of it ?
Ans P4 is Coefficient of x4 . So,when we put i. i4 gives the sign and .
i4 = (i2)2 = (-1)2 = 1
Binomial Series (for negative or fractional indices)
If
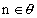and | x | < 1, then(1 + x)n = 1 + nx +
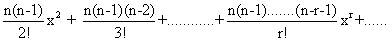
General term = T r+1
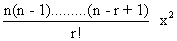
Illustration 9
Find the coefficients of x4andx-4 in expansion of
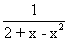, | < x < 2 . =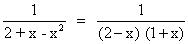
=
=
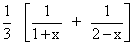
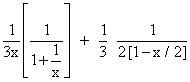
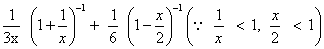
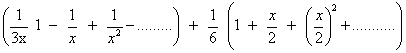
Coefficient of x4 = 0 +
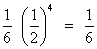
Coefficient of x-4 =
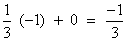
Binomial Theoram
If n is a positive integer then
( a1 + a2 + ........+ am) n
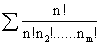a1n1a2n2. a3n3.......am nmWhere the summation is taken over all non-negative integers n1, n2 ..........nm such that n1+ n2 + n3+.....+ nm = n
and the number of terms in the expansion is
= number of non-negative integral soln of equation
n1 + n2 +..........+nm
= n + m -1 Cm-1
Illustration 10 .
find the total number of terms in the kexpansion
of (x + y + z + w) n
Ans. From Hultinomial Theorm
(x + y + z +w )n =
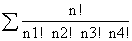x1n1 y n2 zn3 wn4where n1, n2, n3, n4 are non negative integers subject to the condition n1 + n2 + n3 + n4 = n
Hence no of distinct terms
= Coefficient of xnin (xo + x1 + x2 +.......+xn)4
= Coefficient of xn in
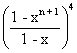
= Coefficient of x nin (1 - xn+1)4 (1 - x)-1
= Coefficient of x nin (1 - x)-4 (since xn+1
= n + 3Cn
=
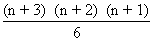
Dumb Question Why is no of disfinft terms equal to coefficient
of xn in (xo + x1 + x2+....................+xn )4 ?
Ans This is actually a problem of permutation and combipnation
But Let us discuss it here very brifly .
Equation is n1 + n2 + n3 + n4 = n
Now n1 can vary from o to n
Similar is the case for n2, n3 and n4.
So, xo + x1 + x2 +..................+ xn for n1
and (xo + x1 + x2 +..................+ x)4 for all n1, n2 + n3 and n4.
And then we try to find coeft of xn as n1 n2+ n3 + n4 head to sum to n
Easy
(1)Prove that Co + C1 + C2+..........Cn = 2n
Ans we know
Co + C1 + C2+..........Cnxn = (1 + x) n
Now put x = 1 or both sides
Co + C1 + C2+..........Cn = 2n
(2) find the sum kof series
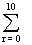20 Cr ? Ans We know =
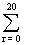20 Cr = 220Now L.H.S. mhas 21lterms out of which 10 pairs are equal.
because nCr= nCn - r
So, L.H.S. 2
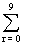20 Cr - 20 C10 = 220So, 2
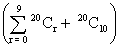= 2 20 + 20 C10or
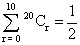(2 20 + 20 C10)