Binomial Theorem - 5
Introduction
(3) Find the digit at unit place in the number .
16 1986 + 111986 - 61986. ?
And Let E = 16 1986 + 111986 - 61986
So, E = (10 + 6)n + (1 + 10)n - 6 n
where N = 1986
= 10N + N C1 10N-1 6 + ..........+ NCN-1 10. 6n-1 + 6N
+ 1 + N C1 10. + N C2 102 + .........+ N CN10 N - 6N
= 1 + All inteqers being multiple of 10
So, The digit at unit place is 1.
(4) Find the value of x for which the sixth term of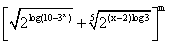
is equal to 21 and binomial coefficient of second, third and fourth terms are first, third and fifth terms of an aritnmetic progression .
Ans The sixth term of the given binomial exponsion is
mC5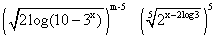
..................(1)
The other given lcondition is, mC1 + mC3 = 2 mC2
=> m2 - 9m + +14 = 0 => (m - 7) (m - 2) = 0
or m = 7 Since m = 2 is not possible .
Put m = 7 in equation (1) to get x = 0, 2
Dumb Question Why m cannot be 2 ?
If m = 2 then there cannot be 6th term in the expansion and hence it is ruled out .
If n is any positive integer show that . 23n+3 - 7n - 8 is divisible by 49 ?
The given expression
= 23n+3 - 7n - 8
= 23(n+1) - 7n - 8
= 8 n+1 - 7n - 8
=(1 + 2)n+1 - 7n - 8
= 8 (1 + 7) n- 7n - 8
= 8 (1 + nC1 7 + n C2. 72........nCn 7n ) - 7n - 8
= 8 + 56n + 8 (nC2 72 ........+ n Cn 7 n ) - 7n- 8
= 49 n 8 (n C2 72 +..............+ n Cn 7n )
= 49 (n + 8 ( n C2 + .......+ n Cn 7 n-2 ) )
So, 23n+3 - 7n - 8 is divisible by 49 .
(6) Find the coefficient of x 50 in the polynoamial
(1 + x) + 2(1 + x)2 + 3(1 + x)3+.........+1000 (1 + x) 1000 ?
Ans Let P(x) = (1 + x) + 2(1 + x)2 + 3(1 + x)3+.........+1000 (1 + x) 1000
Now (1 + x) p(x) - P(x)
= (1 + x)2 + 2(1 + x)3 + 3(1 + x)4 +.........+999 (1 + x) 1000+ 1000(1 + x) 1000
- (1 + x) - 2 (1 + x)2 - 3 (1 + x)3 ....................- 1000 (1 + x)1000
= 1000 (1 + x)1001 - (1 + x) - (1 + x)2 - (1 + x)3-.................-(1 + x)1000
1000 (1 + x) 1001 - [ (1 + x)- (1 + x)2 +.........+ (1 + x)1000]
= 1000 (1 + x)1001-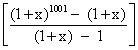
= 1000 (1 + x) 1001 -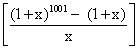
= P(x) =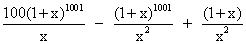
So, coefficient of x50 in P(x)
= 1000 X 1000 C51 = 1000C52
=
=
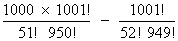
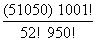
(7) If (1 + x )n = ao + a1x + a2x2+ ..........+an xn then find
value of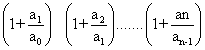
?
Ans Clearly ar = n Cr
So,
=> 1 +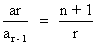
So,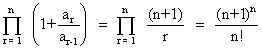
Sum the following series
Co + 5c1 + ac2 + ac2+.........................+(4n + 1)cn
Ans Let S = Co + 5c1 + ac2 + ac2+.........................+(4n + 1)cn............(1)
Sine Cr = Cn -r
So, S Cn + 5Cn-1 + a Cn +.............+ (4n = 1)Co
or S = (4n + 1) Co + (4n - 3) C1+..................+5Cn-1+cn......(2) Now Adding (i) + (2) we get
25 = (4n + 2) Co + C1 +............Cn )
=> S = (2n + 1) 2n
So, Co + 5C1 + 9C2 + ........+ (4n + 1) Cn = (2n + 1) 2n
16 1986 + 111986 - 61986. ?
And Let E = 16 1986 + 111986 - 61986
So, E = (10 + 6)n + (1 + 10)n - 6 n
where N = 1986
= 10N + N C1 10N-1 6 + ..........+ NCN-1 10. 6n-1 + 6N
+ 1 + N C1 10. + N C2 102 + .........+ N CN10 N - 6N
= 1 + All inteqers being multiple of 10
So, The digit at unit place is 1.
(4) Find the value of x for which the sixth term of
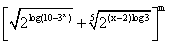is equal to 21 and binomial coefficient of second, third and fourth terms are first, third and fifth terms of an aritnmetic progression .Ans The sixth term of the given binomial exponsion is
mC5
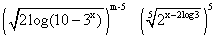..................(1)The other given lcondition is, mC1 + mC3 = 2 mC2
=> m2 - 9m + +14 = 0 => (m - 7) (m - 2) = 0
or m = 7 Since m = 2 is not possible .
Put m = 7 in equation (1) to get x = 0, 2
Dumb Question Why m cannot be 2 ?
If m = 2 then there cannot be 6th term in the expansion and hence it is ruled out .
If n is any positive integer show that . 23n+3 - 7n - 8 is divisible by 49 ?
The given expression
= 23n+3 - 7n - 8
= 23(n+1) - 7n - 8
= 8 n+1 - 7n - 8
=(1 + 2)n+1 - 7n - 8
= 8 (1 + 7) n- 7n - 8
= 8 (1 + nC1 7 + n C2. 72........nCn 7n ) - 7n - 8
= 8 + 56n + 8 (nC2 72 ........+ n Cn 7 n ) - 7n- 8
= 49 n 8 (n C2 72 +..............+ n Cn 7n )
= 49 (n + 8 ( n C2 + .......+ n Cn 7 n-2 ) )
So, 23n+3 - 7n - 8 is divisible by 49 .
(6) Find the coefficient of x 50 in the polynoamial
(1 + x) + 2(1 + x)2 + 3(1 + x)3+.........+1000 (1 + x) 1000 ?
Ans Let P(x) = (1 + x) + 2(1 + x)2 + 3(1 + x)3+.........+1000 (1 + x) 1000
Now (1 + x) p(x) - P(x)
= (1 + x)2 + 2(1 + x)3 + 3(1 + x)4 +.........+999 (1 + x) 1000+ 1000(1 + x) 1000
- (1 + x) - 2 (1 + x)2 - 3 (1 + x)3 ....................- 1000 (1 + x)1000
= 1000 (1 + x)1001 - (1 + x) - (1 + x)2 - (1 + x)3-.................-(1 + x)1000
1000 (1 + x) 1001 - [ (1 + x)- (1 + x)2 +.........+ (1 + x)1000]
= 1000 (1 + x)1001-
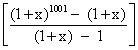
= 1000 (1 + x) 1001 -
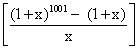
= P(x) =
So, coefficient of x50 in P(x)
= 1000 X 1000 C51 = 1000C52
=
=
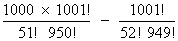
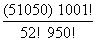
(7) If (1 + x )n = ao + a1x + a2x2+ ..........+an xn then find
value of
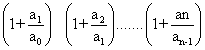?Ans Clearly ar = n Cr
So,
=> 1 +
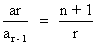
So,
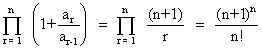
Sum the following series
Co + 5c1 + ac2 + ac2+.........................+(4n + 1)cn
Ans Let S = Co + 5c1 + ac2 + ac2+.........................+(4n + 1)cn............(1)
Sine Cr = Cn -r
So, S Cn + 5Cn-1 + a Cn +.............+ (4n = 1)Co
or S = (4n + 1) Co + (4n - 3) C1+..................+5Cn-1+cn......(2) Now Adding (i) + (2) we get
25 = (4n + 2) Co + C1 +............Cn )
=> S = (2n + 1) 2n
So, Co + 5C1 + 9C2 + ........+ (4n + 1) Cn = (2n + 1) 2n