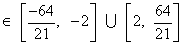study material-mathematics-algebra-binomial theorem
Binomial Theorem - 6
(9) If is an odd natural lnumber then what is the value
Of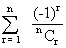 
?
Ans Since n is odd, the number of terms will be n + 1 which is even, Now since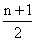 
is an integer we make pairs of terms equidistant from the beginning and end .
So,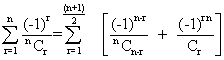 
(-1) r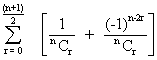 
(-1) r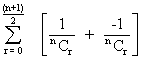
= 0
f
Hence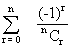 
= 0
Dumb Question : Why (-1) n-2r is -1 for all v )
Ans Since n is odd so, n - 2r is odd as 2r is even .
Thus (-1) odd = -1 .
(10) find the sum of the series .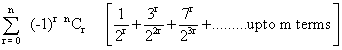
Ans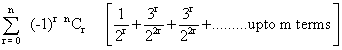 
= 
= 
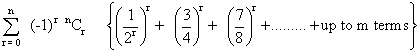
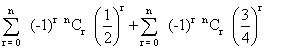+…………up to m terms
= 
=
= 
= 
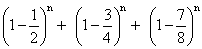
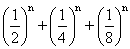
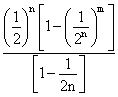
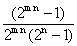
(11) Prove the following identity
n Co + n+1 C1 + n+2 C2+………..+n+r Cr = n+r+1 Cr
Ans n Co is coefficient of xn in expansion of (x + 1)n
n+1 C1 is coefficient of xn in expansion of (x + 1)n+1
…………………………………………………………..
n+r Cr is coefficient of (x + 1) n+r
Thus L.H.S. is coefficient of xn inexpansion of
(x + 1)n + (x + 1)n+1 +…………….+ (x + 1)n+r
Or coefficient of xn in (x + 1) n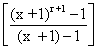 
Or coefficient of xn in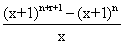 
Or coefficient of xn+1 in (x + 1)n+r+1 - (x - 1) n
=n+r+1 cn+1 (since (x + 1)n has no ten containing x n+1 )
= n+r+1Cr
Medium.
(1) Given that 4th term in expansion of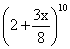 
has the maximum numberical value, find the range of value of x for which this will be true .
Ans According to the question
| t4 |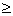 
| t3 |, | t4 | 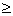| t5 |
Now, tr+1 = 10Cr210-r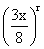 
t4 = 10 C3 27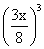 
t 3 = 10 C2 28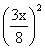 
and t5 =10 C2 26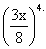 
Now, | t4 |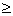 | t3 |
=> 10 C3 27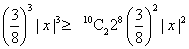 
=> | x | 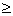2 ………..(1)
and | t4 | 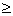| t5 |
10C3 27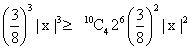
=> 
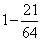| x | 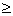0 ………….(2)
Clearly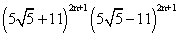 
= 
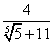
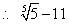is a positive proper fraction
and so g =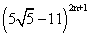 
is also a positive proper fraction.
Thus, 0 < f < 1 and 0 < g < 1
Now, [R] + f - g
= 2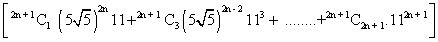 
= 2 X inteqer = even integer.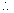
f - g must be an integer because [R] is ans itneger .
Now f - g = 0 i.e f = g .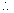
R. F{ [R] + f } = ( [R] + f ) g
=
=
= 
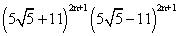
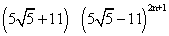
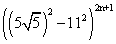
= 4 2n + 1
Dumb Question.
Why f - g is zero ?
Thus we get | x |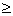 2 and | x |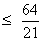 
So, x