Binomial Theorem - 7
Dumb Question
Why we had an interval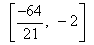
in answer ?
Ans . Well we have the situation
| x |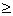
2 and 
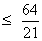
So, | x |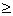 2 means
x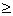 2 or x 
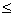- 2
Similariey | x |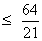
and hence we get the interal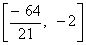
(2) Let R =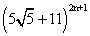
and F = R - [R] where [] denotes the greatest integral funftion. Prove that RF = 42n+1.
Ans R = [R] + F =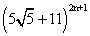
= 2n+1Co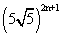
+ 2n+1C1 
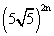. 11 +............+ 2n+1C2n+1 112n+1 .....................(1)
Let g =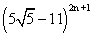
= 2n+1 Co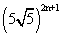 - 2n+1 C1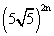11 +............+ 2n+1C2n+1 112n+1 .....................(2)
F and g both are positive proper fraction. i.e.
O < f < 1, O< g < 1
So, F - g con not be any integer exept zero because where both f and g not kintegers how can there difference be.
(3) If (1 + x + x2)n = ao + a1x + a2x2 + a3 x3 +........+ a2nx
2n then show that
ao + a3 + a6 +..........=a1 + a4 + a7 +.............
= a2 + a5 + a8 + .....................
Ans Putting x = 1, w, w2 where w is a non ,real cine root of unity ?
So, Zn = ao + a1 + a2 +..................................(1)
O = a0+ a1 w + a2 w2+ ..............(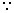
+ w + w2 = o ) .......(2)
0 = a0 + a1 w2 + a2 w4 ...............(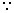 1 + w + w2 = 0 ) ...........(3)
Adding these .
3n 3 a0 + a1 (1 + w + w2) + a2 (1 + w + w4 ) + a3 (1 + w3+ w6) + .........
= 3(a0 + a3 + a6 +................)
=>a0 + a3 + a6 + ...........3n-1
from (1) + (2) X w2 + (3) X w.......we get
3n + O X w2 + O X W
= a0 (1 + w2 + w ) + a1 (1 +w3+ w3 ) + a2 (1 + w4 + w5 + a3 (1+ w5 + w7) + a4 (1 + w6 + w9 ) +.........
img..........3n = 3(a1 + a4 + a7 + ..............)
So, a1 + a4 + a7 + .................3n-1
Again from (1) + (2) x w + (3) w2 we get
3n = a0 (1 + w + w2 ) + a1 (1 + w2 + w4 ) +a2 (1 + w 3 + w3 ) +.........
= 3(a2+ a5 a8+..........)
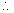a2 + a5 + a8 +..............=3n-1
Dumb Question.
Why 1 + w4 +w5 is equal to zero and
1 + w6 +w9 is 3.?
1 + w4 +w5 = 1 + w +w2 (using w3 = 1 )
= 0
Also 1 + w6 +w9 = 1 + (w3) 2 + (w3) 3
= 1 + 1 + 1
= 3 .
(4) Find the value of C0 - C1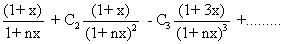
Ans . Let Co - C1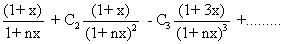
=
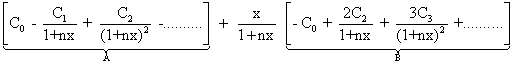
So, (1 - y)n = C0 - C1 y + C2y2 - C3 y3 +........(-1)n yn
defferentiating w.r.t. y we get
-n (1 - y)n-1 = - C1 + 2C2 y - 3C3 y2 +............
Now A =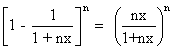
and B = -C2 + 2C2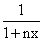
= - n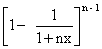
= - n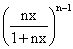
So, C0 - C1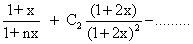
= A +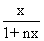
B
=
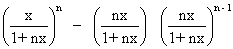
= 0
(5) Prov that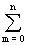
n Cm sin (mx) cos ((n-m)x) = 2n-1 sin <(nx)
Ans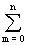n Cm sin (mx) cos (n - m) x.
= n C0 (0.x ) cos nx + nC1 sin x ccos (n -1) x
=n C2 sin 2x cos (n - 2) x + .................
.................= n Cn sin nx cos (0 . x)
=> 2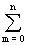n Cm sin (m x) cos (n - m) x
[ n C0 (0 . x) cos nx + n sin nx cos 0 . x]
+ [ n C1 sin x cos (n - 1) x + n Cn-1 sin (n - 1) x . cos x ]
......+ [n Cn sin nx cos(0 . x) + nC0 sin (0 . x) cos nx ]
Using n Cr = n Cn-r we get
2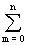n Cm sin (m x) cos (n - m ) x
= n C0 [ sin (0 . x) cos (n x) + sin (n x) cos (0 . x)]
+ n C1 [ sin x cos (n -1) x + sin (n - 1) x cosx ] + .......
...........+ n Cn[ sin x cos (0 . x) + cos (n x )sin (0 . x)]
NOw using sin (A + B) = sinA cos B + cosA sinB we get
( n C0 + n C1 + n C2 +.................+n Cn ) sin nx = 2n sin nx.
So,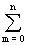n Cm sin (m x) cos (n - m) x = 2n-1 sin (nx)
(6) If an =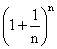
then prove that 2 < an < 3 img......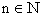
Why we had an interval
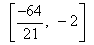in answer ?Ans . Well we have the situation
| x |
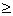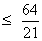
2 and So, | x |
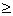2 means x
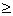2 or x 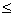- 2Similariey | x |
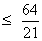
and hence we get the interal
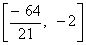
(2) Let R =
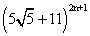and F = R - [R] where [] denotes the greatest integral funftion. Prove that RF = 42n+1. Ans R = [R] + F =
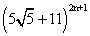
= 2n+1Co
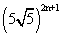+ 2n+1C1 . 11 +............+ 2n+1C2n+1 112n+1 .....................(1)Let g =
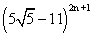
= 2n+1 Co
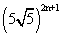- 2n+1 C111 +............+ 2n+1C2n+1 112n+1 .....................(2)F and g both are positive proper fraction. i.e.
O < f < 1, O< g < 1
So, F - g con not be any integer exept zero because where both f and g not kintegers how can there difference be.
(3) If (1 + x + x2)n = ao + a1x + a2x2 + a3 x3 +........+ a2nx
2n then show that
ao + a3 + a6 +..........=a1 + a4 + a7 +.............
= a2 + a5 + a8 + .....................
Ans Putting x = 1, w, w2 where w is a non ,real cine root of unity ?
So, Zn = ao + a1 + a2 +..................................(1)
O = a0+ a1 w + a2 w2+ ..............(
+ w + w2 = o ) .......(2)0 = a0 + a1 w2 + a2 w4 ...............(
1 + w + w2 = 0 ) ...........(3) Adding these .
3n 3 a0 + a1 (1 + w + w2) + a2 (1 + w + w4 ) + a3 (1 + w3+ w6) + .........
= 3(a0 + a3 + a6 +................)
=>a0 + a3 + a6 + ...........3n-1
from (1) + (2) X w2 + (3) X w.......we get
3n + O X w2 + O X W
= a0 (1 + w2 + w ) + a1 (1 +w3+ w3 ) + a2 (1 + w4 + w5 + a3 (1+ w5 + w7) + a4 (1 + w6 + w9 ) +.........
img..........3n = 3(a1 + a4 + a7 + ..............)
So, a1 + a4 + a7 + .................3n-1
Again from (1) + (2) x w + (3) w2 we get
3n = a0 (1 + w + w2 ) + a1 (1 + w2 + w4 ) +a2 (1 + w 3 + w3 ) +.........
= 3(a2+ a5 a8+..........)
a2 + a5 + a8 +..............=3n-1Dumb Question.
Why 1 + w4 +w5 is equal to zero and
1 + w6 +w9 is 3.?
1 + w4 +w5 = 1 + w +w2 (using w3 = 1 )
= 0
Also 1 + w6 +w9 = 1 + (w3) 2 + (w3) 3
= 1 + 1 + 1
= 3 .
(4) Find the value of C0 - C1
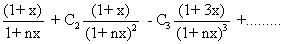
Ans . Let Co - C1
=
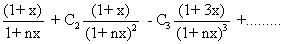
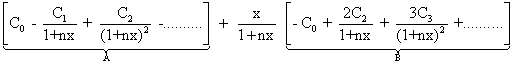
So, (1 - y)n = C0 - C1 y + C2y2 - C3 y3 +........(-1)n yn
defferentiating w.r.t. y we get
-n (1 - y)n-1 = - C1 + 2C2 y - 3C3 y2 +............
Now A =
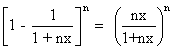
and B = -C2 + 2C2
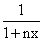
= - n
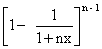
= - n
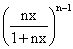
So, C0 - C1
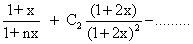
= A +
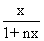B=
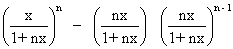
= 0
(5) Prov that
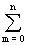n Cm sin (mx) cos ((n-m)x) = 2n-1 sin <(nx) Ans
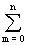n Cm sin (mx) cos (n - m) x.= n C0 (0.x ) cos nx + nC1 sin x ccos (n -1) x
=n C2 sin 2x cos (n - 2) x + .................
.................= n Cn sin nx cos (0 . x)
=> 2
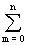n Cm sin (m x) cos (n - m) x [ n C0 (0 . x) cos nx + n sin nx cos 0 . x]
+ [ n C1 sin x cos (n - 1) x + n Cn-1 sin (n - 1) x . cos x ]
......+ [n Cn sin nx cos(0 . x) + nC0 sin (0 . x) cos nx ]
Using n Cr = n Cn-r we get
2
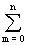n Cm sin (m x) cos (n - m ) x = n C0 [ sin (0 . x) cos (n x) + sin (n x) cos (0 . x)]
+ n C1 [ sin x cos (n -1) x + sin (n - 1) x cosx ] + .......
...........+ n Cn[ sin x cos (0 . x) + cos (n x )sin (0 . x)]
NOw using sin (A + B) = sinA cos B + cosA sinB we get
( n C0 + n C1 + n C2 +.................+n Cn ) sin nx = 2n sin nx.
So,
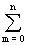n Cm sin (m x) cos (n - m) x = 2n-1 sin (nx) (6) If an =
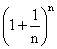then prove that 2 < an < 3 img......