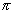Binomial Theorem - 8
Also show that
nn-1 > (n + 1)n ; 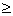 3 ,
3 , 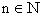
Ans . We get an = 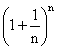
= 1 + n 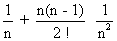 + …………………
+ …………………
= 1 + 1 + 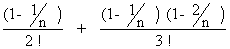 + …………..
+ …………..
= 2 + Positive quantity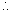 an > 2 . ……………(1)
an > 2 . ……………(1)
Alos, an < 1 + 1 + 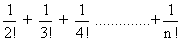
< 1 + 1 +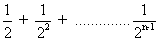
< 1 +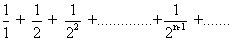
< 1 + 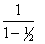
< 3 ……………….(2)
From (1) and (2) we get
2 < an < 3
So, an < 3
Or 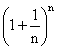 < 3
< 3
or 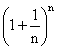 < n (
< n ( n
n  3 )
3 )
or……….img
So, (1 + )n < n4. n
or (n + 1)n < nn+1
Dumb Question
Why img……….
img…………
Ans We are dividing one by a smaller no because all natural no.s except 2 are bigger than 2 only
So, 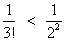
as 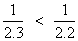
3 > 2 so, 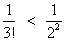
For other factor also
So, 1 + 1 + 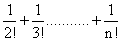 is less than 1 + 1 +
is less than 1 + 1 + 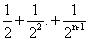
Hard
(1) Prove that 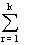 (-1 ) r-1 3n C2r-1 = 0 where k=
(-1 ) r-1 3n C2r-1 = 0 where k= 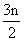
is an even positive inteqer.
Ans Given n is an even positive inteqer.
Let n = 2m 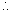 R = 3m
R = 3m 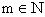
L.H.S.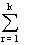 (-3)r-1 3nC 2r-1 =
(-3)r-1 3nC 2r-1 = 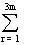 (-3) r-1 6m C2r-1
(-3) r-1 6m C2r-1
= 6m C1 - 3 6m C3 + 32 6m C5-……..+ (-3)3m-16m C6m -1 ……….(1)
(1 + i 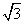 ) 6m = 6m Co + 6m C1 (i
) 6m = 6m Co + 6m C1 (i 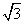 ) + 6m C2 (i
) + 6m C2 (i 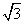 )2+ ………+ 6mC6m-1(i
)2+ ………+ 6mC6m-1(i 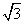 ) 6m-1+ 6m C6m(i
) 6m-1+ 6m C6m(i 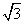 )6mimg …………….
)6mimg …………….
or 26m 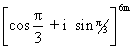 =6m Co + 6m C1 (i
=6m Co + 6m C1 (i 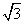 ) + 6m C2 (i
) + 6m C2 (i 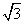 )2+ ………+ 6mC6m-1(i
)2+ ………+ 6mC6m-1(i 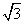 ) 6m-1+ 6m C6m(i
) 6m-1+ 6m C6m(i 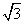 )6m
)6m
or 26m( cos 2 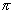 + i sin 2
+ i sin 2 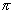 m )
m )
=( 6mCo - 3 6m C2 + 32 6m - …..+ (-3) 3m 6m C6m) + i 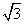 ( 6mCo - 3 6m C2 + 32 6m - …..+ (-3) 3m 6m C6m)
( 6mCo - 3 6m C2 + 32 6m - …..+ (-3) 3m 6m C6m)
Companing imaqinary part on both sides we get .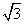 ( 6m C1 - 3 6m C3 +32 6mC5………..+ (-3) 3m-1 6mC6m-1 ) = 0
( 6m C1 - 3 6m C3 +32 6mC5………..+ (-3) 3m-1 6mC6m-1 ) = 0
Or ( 6m C1 - 3 6m C3 +32 6mC5………..+ (-3) 3m-1 6mC6m-1 ) = 0
=> 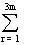 (-3) r-1 6m C2r-2 = 0
(-3) r-1 6m C2r-2 = 0
Or 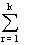 (-33) r-1 3n C2r-1 = 0 (where n = 2m)
(-33) r-1 3n C2r-1 = 0 (where n = 2m)
Dumb Question: How did ( cos 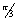 + i sin
+ i sin 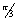 ) 6m be came cos 2
) 6m be came cos 2 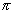 m + i sin2
m + i sin2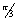 m ?
m ?
inmg……..
Ans We used Eulers Rule which is (( cos 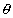 + sin
+ sin 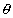 ) m = cosm
) m = cosm 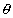 +sin
+sin 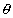
So, ( cos 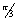 + i sin
+ i sin 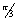 ) 6m = cos 6m
) 6m = cos 6m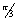 + i sin 6m
+ i sin 6m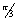 )
)
= cos 2m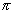 + i sin 2m
+ i sin 2m