Binomial Theorem - 9
(2) If n > 3 then prove that
C0 ab - C1(a - 1) + C2 (a - b) (b - 2) - ……………+ (-1) n Cn = 0
Ans Now, (1 + x)n = 1 + nx +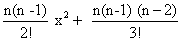 
x3 +……….+x put x = - 1
0 = 1 - n +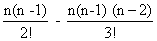 
+ ……….++ (-1) n ……………….(1)
Now replace n by n - 1
So, 0 = 1 - (n - 1) +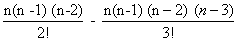 
+……………..+ (- 1) n-1…………..(2)
Multiplying (1) by a and (2) by n and odding we get.
a - na +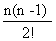 
a + ……………..+ (-1)na + n - n(n -1) +
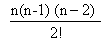- …………+ (-1)n-1n = 0
=> a - n (a-1)+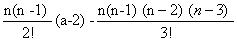 
-………..+(-1) n(a-n) = 0………………..(3)
Now Replace n by n-1 and a by a-1 in (3) to get
(a - 1) - (n - 1) (a - 2) + 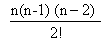(a - 3) + ……..+ (-1) n-1 (a - n) = 0……(4)
Multiplying (3) by b and (4) by n we get .
ab - n(a - 1) b + 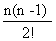(a - 2)b +………..+(-1)n (a - n)b
- n(a - 1) -n (n - 1)(n - 2)+………..+(-1)n-1 (a - n)n = 0
On the other hand
(……(((x - 2)2 - 2 )2 -……….-2)2
= ((……((x - 2)2 - 2 )2 -……..-2)2-2)2
k - 1tirmes
= [ ( Rk-1x3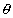
x2 + Rk-1 x + 4) - 2 ]2
= ( Rk-1x3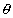x2 + Rk-1 x + 2)2
= R2k-1 x6 + 2Rk-1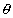k-1x5+ (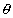k-12+ 2pk-1Rk-1) x4
- (4R k-1 + 2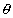k-1Pk-1) x3
- (Pk-12 4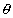k-1) x2 + 4Pk-1x + 4 .
= [R2 k-1x3 + 2Rk-1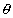k-1 x2 + (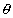2k-1+ 2Pk-1 Rk-1) x+4R k-1 + 2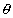k-1Pk-1)] x2
+(Pk-12 4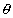k-1) x2 + 4Pk-1x + 4 .
Whence Pk = 4Pk-1 and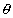k= P2k-1+4 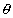k-1
Since (x - 2)2 x2 4x + 4
We have P1 = - 4.
So, P2 = - 42, P3 = - 43………..
and so, Pk = - 4k
NOw let us compute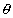k
= P2 k-1 +4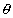k-1
=>P2 k-1 +4(P2 k-1 +4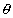k-2)
Pk-12 + 4 (Pk-22 + 4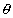k-2)
= Pk-12 + 4 Pk-22 + 42 Pk-32 +………….+4k-2P1 + 4k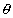-11
=> ab - n (a - 1)(b - 1)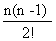 (a - 2)(b - 2)…………+ (-1)n
Or. C0 ab - C1(a - 1) (b - 1) + C2 (a - 2)(b - 2)………
+(- 1)n Cn (a - n) b - n) = 0
(3) Determine coefficients in x2 appeating parantheses have been removed and like terms have been callected is the expression
(.........(( x - 2)2 - 2)2 .........-2 )2
Ans Let us first of all determine constant term which is obtained from the expression.
[ (( x - 2)2 - 2)2 .........-2 ]2
k times
For kthis we put x = 0 i.e it is equal to
(.........((- 2)2 - 2)2 .........-2 )2
k times
(.........(( 4 - 2)2 - 2)2 .........-2 )2
(R -1)times
= (......(4 - 2)2-............-2)2
(R - 2) times
=((4 - 2)2 - 2)2 = (4 - 2)2 = 4
Now let us denote ny Pk the coe fficient of x by Pkthe coefficient of x2 and the Rk the coefficient of x3 the sum of terms involving x to the powers higher than 2 then we can write
(.........(( x - 2)2 - 2)2 -.........-2 )2= Rk x3 + 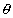kx2 +Pkx + 4
Now by substituting img ..........= 1, P1 = - 4, P2 =-42.....
into this expression we get,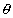
k= 42k-2 + 4.42k-4+ 42 42k-6+........4k-2 42 + 4k-1 1.
= 42k-2 + 4.42k-3+ 42 42k-4+........4k ++4k-1
= 4k-1 [ 1 + 4 + 42 +..........+4k-1]
=4k-1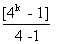 
= 
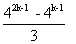
So, Coefficient of x2 in the given expression is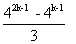
Dumb Question. What is the significance of the subscript in Rk ,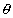k , Pk etc?
Ans One may note that the expression in a very symetric kind of fexpression where things are repeated k times The subscript k denotes that repetition olnly .
One should always remember that symetry isan important thing in matrematics and should be always used aas an important tool
Key words
(1) Binomial theoram
(2) Binomial Coefficient .
(3) General term .
(4) Multinormial theoram.
(5) Binomial series.
(6) Middle term.