study material-physics-modern physics
BOHR MODEL & X-RAYS - 4
MOSELEY’S LAW FOR CHARACTERISTIC X-RAY:-
Moseley measured the frequency of characteristic X-rays from a large number of elements and plotted the 
Vs Z. The plot was close to a straight line (emission was for Kd line).
Moseley forwarded his law of the frequency of Kd lin:-
= a(Z - 1) = 4.98 x 107(Z - 1)
where ‘a’ is a constant
for general characteristic X-rays, Moseley’s law is
= a(Z - b) b is another constant.
ILLUSTRATION:- Use Moseley’s law with b = 1 to find the frequency of the Kd X-rays of La(Z = 57) if the frequency of Kd X-rays of Cu(Z = 2a) is known to be 1.88 x 1018 Hz.
Solution:- Using equation = a(Z - b)
PROBLEM:-
Easy:- 1. An experiment measuring the Kd line of Fe yields 1.94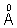 
. Determine atomic number of iron.
Solution:- From Moseley law
= (4.97 X 107)(Z - 1) or Z = i + 
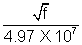
also f =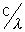 
We get Z = 1 + 
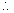Z = 260.2 
26 (atomic number of iron)
2. Stopping potential of 24, 100, 110 and KV are measured for electrons emitted from o certain element when it is irradiated with monochromatic X-ray. If this element is used as target in an X-ray tube, What will be the waavelength of the 
line.
Solution:- The stopping energy, eVs is equal to the difference between the energy of the incident photon and the binding energy of the electron in a particular shell.
eVs = EP - EB
The different stopping potential arise from electrons being emitted from different shells, with the smallest value (24 KV) corresponding to ejection of a K - shell electron. Subtrating the expression for the two smallest stopping potentials, we obtain
eVSL - eVSK = (EP - EBL) - (EP - EBK) = EBK - EBL
or 100 KeV - 24 KeV = EBK - EBL
The difference, 76 KeV is the energy of the Kd line. The corresponding wavelength is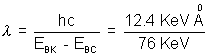
= 0.163
3. The wavelength of the first member of the balmen series in hydrogen spectrum is 6563 . What is the wavelength of the first member of Lymen series ?
Solution:- Balmen series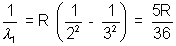 
Lymen series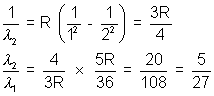
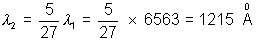
4. The wavelength of Kd X-rays tungsten is 0.21 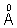. If the enrgy of tungsten atom with an L electron knocked out in 11.3 KeV. What will be the energy of this atom when a K electron is knocked out ?
Solution:- Energy of Kd photon : E = 
=> E =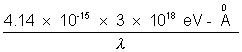 
= 59.1 KeV
Let EK = energy of the with a vacancy in the K - shell
EL = energy of the atom with vacancy in the L - shell.
Then EK - EL = E => EK + EL = 59.1 + 11.3 = 70.4 KeV