BOHR MODEL & X-RAYS - 7
HARD:-
1. An imaginary particle has a charge equal to that of an electron and mass 100 times the man of the electron. If moves in a circular orbit around a nucleus of charge + 4e. Take the mass of the nucleus to be infinite. Assuming the Bohr's model is applicable to this system.
(a) Derive an expression for the radius of nth Bohr orbit.
(b) Find the wavelength of the radiation emitted when the particle jumps from fourth orbit to the second orbit.
Solution:- (a) We have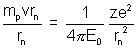 ....................... (i) [Centripetal force]
....................... (i) [Centripetal force]
The quantization of angular momentum gives,
mpvrn =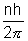 .................................... (ii)
.................................... (ii)
Solving (i) & (ii), we get
r =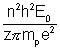 ..................................... (iii)
..................................... (iii)
Substituting mp = 100 m and Z = 4
(where m = mass of electron)
We get, rn =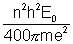
(b) As we know, E1H = - 13.60 eV
and En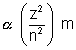
for the given particle, E4 =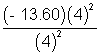 x 100 = - 1300 eV
x 100 = - 1300 eV
E2 =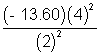 x 100 = - 5440 eV
x 100 = - 5440 eV
 E = E4 - E2 s= 4080 eV
E = E4 - E2 s= 4080 eV
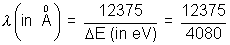 = 3.0
= 3.0 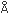
2. The energy levels of hypothetical are electron atom are given by
En = -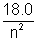 eV
eV
where n = 1, 2, 3 .......................
(a) Compute the four lower energy level diagram.
(b) What is the excitation potential of the stage n = 2 ?
(c) What wavelength (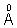 ) can be emitted when then atoms in the ground state are bombarded by electrons that have been accelerated through a potential difference of 16.2 V.
) can be emitted when then atoms in the ground state are bombarded by electrons that have been accelerated through a potential difference of 16.2 V.
Solution:- (a) E1 =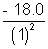 = - 18.0 eV
= - 18.0 eV
E2 =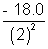 = - 4.5 eV
= - 4.5 eV
E3 =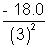 = - 2.0 eV
= - 2.0 eV
and E4 =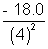 = - 1.125 eV
= - 1.125 eV
The energy level diagram is shown below.
Diagram
(b) The excitation potential of stage n = 2 is 18.0 - 4.5 = 13.5 Volts.
(c) Energy of the electron accelerated by a potential diffrence of 16.2 V is 16.2 eV with this energy the electron can write the atom from n = 1 to n = 3 as
E4 - E1 = - 1.125 - (- 18.0) = 16.875 eV > 16.2 eV
and E3 - E1 = - 2.0 - (- 18.0) = 16.0 eV < 16.2 eV
Now,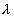 32 =
32 = 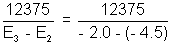 = 4950
= 4950  Ans.
Ans.
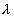 31 =
31 = 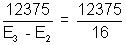 = 773
= 773  Ans.
Ans.
and 21 =
21 = 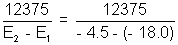 = 917
= 917 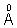
1. An imaginary particle has a charge equal to that of an electron and mass 100 times the man of the electron. If moves in a circular orbit around a nucleus of charge + 4e. Take the mass of the nucleus to be infinite. Assuming the Bohr's model is applicable to this system.
(a) Derive an expression for the radius of nth Bohr orbit.
(b) Find the wavelength of the radiation emitted when the particle jumps from fourth orbit to the second orbit.
Solution:- (a) We have
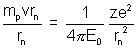 ....................... (i) [Centripetal force]
....................... (i) [Centripetal force]The quantization of angular momentum gives,
mpvrn =
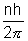 .................................... (ii)
.................................... (ii)Solving (i) & (ii), we get
r =
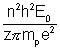 ..................................... (iii)
..................................... (iii)Substituting mp = 100 m and Z = 4
(where m = mass of electron)
We get, rn =
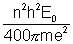
(b) As we know, E1H = - 13.60 eV
and En
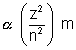
for the given particle, E4 =
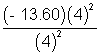 x 100 = - 1300 eV
x 100 = - 1300 eVE2 =
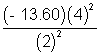 x 100 = - 5440 eV
x 100 = - 5440 eV E = E4 - E2 s= 4080 eV
E = E4 - E2 s= 4080 eV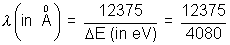 = 3.0
= 3.0 2. The energy levels of hypothetical are electron atom are given by
En = -
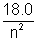 eV
eVwhere n = 1, 2, 3 .......................
(a) Compute the four lower energy level diagram.
(b) What is the excitation potential of the stage n = 2 ?
(c) What wavelength (
 ) can be emitted when then atoms in the ground state are bombarded by electrons that have been accelerated through a potential difference of 16.2 V.
) can be emitted when then atoms in the ground state are bombarded by electrons that have been accelerated through a potential difference of 16.2 V.Solution:- (a) E1 =
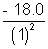 = - 18.0 eV
= - 18.0 eVE2 =
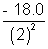 = - 4.5 eV
= - 4.5 eVE3 =
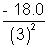 = - 2.0 eV
= - 2.0 eVand E4 =
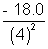 = - 1.125 eV
= - 1.125 eVThe energy level diagram is shown below.
Diagram
(b) The excitation potential of stage n = 2 is 18.0 - 4.5 = 13.5 Volts.
(c) Energy of the electron accelerated by a potential diffrence of 16.2 V is 16.2 eV with this energy the electron can write the atom from n = 1 to n = 3 as
E4 - E1 = - 1.125 - (- 18.0) = 16.875 eV > 16.2 eV
and E3 - E1 = - 2.0 - (- 18.0) = 16.0 eV < 16.2 eV
Now,
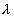 32 =
32 = 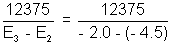 = 4950
= 4950  Ans.
Ans. 31 =
31 = 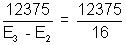 = 773
= 773  Ans.
Ans.and
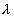 21 =
21 = 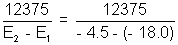 = 917
= 917