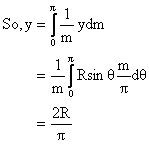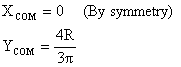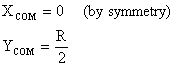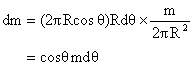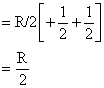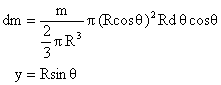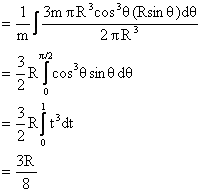study material-physics-mechanics-centre of mass
Center Of Mass -2
| Center of mass, Momemtum, Collision |
|
Introduction
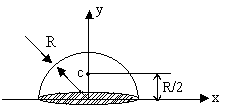
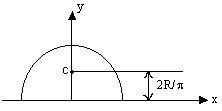
B)
Derivation:
Total length of semi circular wire = Elemental length = Rdq So
C)
Derivation:
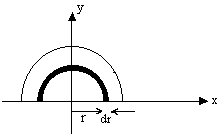
Here the element chosen is a thin wire (semi circular) of radius r. As derived earlier, the
Dumb Question: <!--[if !supportLists]--> 1) Why is Ans: The mass dm is a semi circular thin wire whose position is variable (y is not unique), so we concentrate dm mass on the COM of this wire that is at
D)
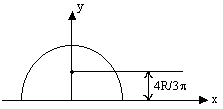
Derivation:
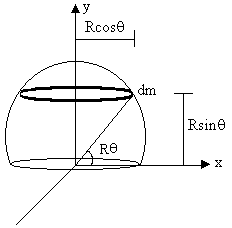
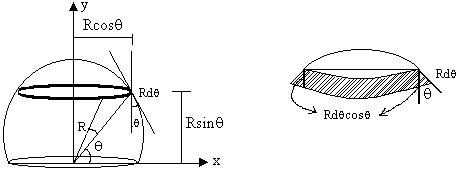
Dumb Question: <!--[if !supportLists]--> 1) Why is y = Rsinq here? Ans: The Center of Mass of elemental ring is at its center (by symmetry) which is at a height of Rsinq from origin; hence y = Rsinq.
E)
Derivation:
Dumb Question: <!--[if !supportLists]--> 1) Why is volume of elemental disc = Rdq (cosq) (pR2cos2q) and not Rdq (pR2cos2q)? Ans: This is a solid hemisphere. If we consider the curvature at the ends of the disc as negligible (as we do in a hollow shell as in the previous case) then the integration starts yielding wrong results. So as a tip we can take this that whenever the integration is being done over solid objects, the curvature effects cannot be neglected!
|
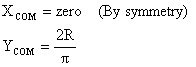
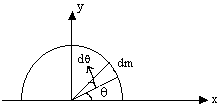
 R
R