VARIABLE MASS:
These are the systems in which mass does not remain constant with respect to time.
Basic Equation:
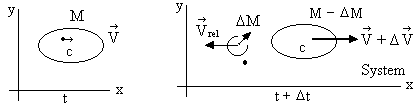
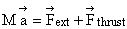
Derivation:
The two states of the system are shown at instants t and t + Dt. Initially whole mass M moves with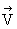 
. After Dt time, DM moves with relative velocity 
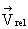while rest (M-DM) moves with 
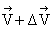. Note that absolute velocity of DM is 
.
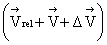On the system
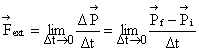
Now,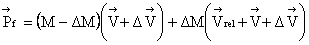 
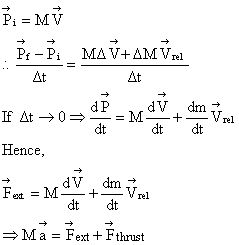
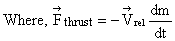
Note: Here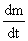 
is negative, so thrust force becomes +ve.
Illustration: A rocket of initial mass m0 (including shell and fuel) is fired vertically at time t = 0. The fuel is consumed at a rate of ‘a = At’ where A = constant, t = time. The gases are exhaust at a constant relative speed of ‘m’ m/s with respect to rocket. In addition to gravity, there is resistance from air which can be assumed to be a constant force of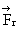 
. Find the differential equation velocity of rocket at the time t?
Solution:
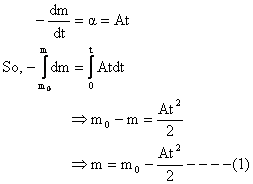
{This is the mass at time t}
Let the velocity of rocket at time ‘t’ = V.
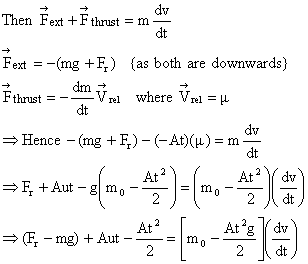
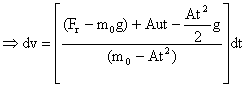
This is the differential equation governing the velocity of rocket with respect to time.
Illustration:
The chain has mass per unit length = M kg/m. What should be the value of F so as to pull the chain with constant velocity v?
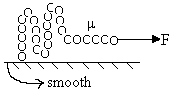
Solution:
Let at the time t
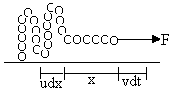
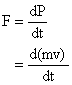
Dumb Question:
<!--[if !supportLists]--> 1) What is ?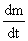
Ans: If ‘dx’ length is also set into motion then mdx mass is set into motion.
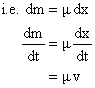
<!--[if !supportLists]--> 2) What is the system here?
Ans: The system can be the chain that is being set into motion. Solving with time, the system is increasing in length and hence mass!