IMPULSUE:
Impulse is defined as the product of force and time. If force is constant then,
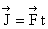. Here time ‘t’ is the time for which force acts.
On the other hand if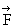 
is not constant then 
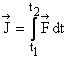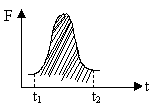
where 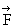acts between time t1 and t2. This also represents the area under F-t graph with end points t1 and t2.
Dumb Question:
<!--[if !supportLists]--> 1) A man who falls from a height on a cement floor receives more injury than when he falls from same height on a heap of sand why?
Ans: Just before the collision the velocity of man is same in both cases. Now the momentum of man has to come to zero, so to change momentum either a large force can be applied in a short interval of time or a smaller force in a large interval of time. In case of cement does not deform. But sand deforms to same extent there by extending the time period. Hence force applied is lesser here.
COLLISION:
Collision can be defined as an event of short duration during which the colliding bodies exert large force on each other. During the collision the total momentum of system does not change. If no external forces are acting on the system. The impulsive forces acting during the collision are internal forces which have no effect on total momentum of system.
Collision – Elastic (Coefficient of restitution = 1) (No Loss of K.E)
- Inelastic (Coefficient of restitution < 1) (Loss of K.E)
Collision - Head on (Directions of velocities are along the line of impact)
- Oblique (Otherwise)
Coefficient of restitution is defined as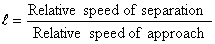 
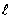=1 Perfectly Elastic Collision
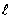=0 Perfectly Inelastic Collision
1) Head on Elastic Collision:
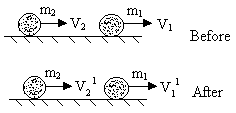
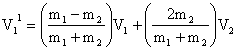
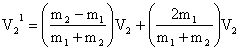
Derivation:
System = m1+m2; so momentum is conserved.
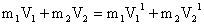------- (1)
As elastic collision so (K.E) initial = (K.E) final
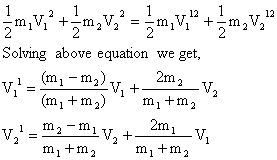
Note:
<!--[if !supportLists]--> a) When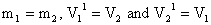 
i.e. velocities get exchanged.
<!--[if !supportLists]--> b) If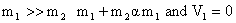 
.
.
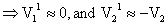That is the smaller ball rebounds with same velocity while bigger one which was at rest remains at rest.
c)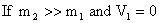 
.
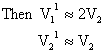
That is the bigger ball keeps on moving with same velocity while other moves with 2V2.
2) Head on Inelastic Collision:
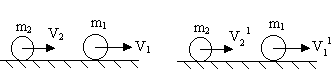
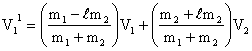
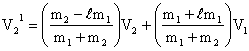
Derivation:
The two balls together form the system so linear momentum is still conserved.
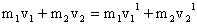------------ (1)
Now K.E doesn’t remain constant because there is loss of energy.
The second equation comes from
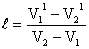-------- (2)
Solving these two we get above results.
Illustration:
A ball of mass m0 at a speed V0 makes a head on collision with an identical ball at rest. KE of balls after the collision is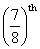 
of the original. Find the coefficient of restitution?
Solution:
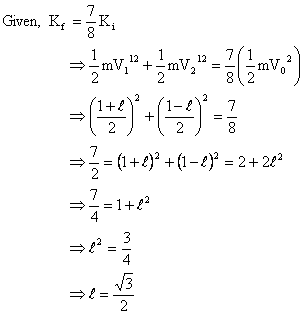
OBLIQUE COLLISIONS:
When at least one body moves in a direction different from the line of impact, the collision is called oblique. In oblique collisions;
<!--[if !supportLists]--> a) Impulses act along common normal and momentum is conserved in this direction.
<!--[if !supportLists]--> b) No impulse act in tangential direction.
<!--[if !supportLists]--> c) Definition of coefficient of restitution is applied only in normal direction.
<!--[if !supportLists]--> d) Net momentum is conserved.
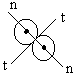
Illustration:
The ball of mass m0 hits a floor with speed m at an angle q. The coefficient of restitution is 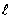. Find ‘f’ and velocity ‘v’?
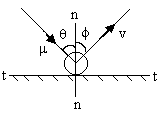
Solution:
In n-n direction:
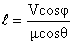--------- (1)
In t-t direction:
mSinq = Vsinf -------- (2)
Solving (1) and (2) we get
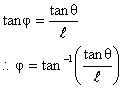
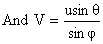
Where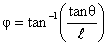 
.
Dumb Question:
<!--[if !supportLists]--> 1) Why the velocity component in t-t direction does does not change?
Ans: Because there is no impulse in t-t direction hence momentum remains
mSinq = Vsinf.