Circles - 1
Introduction
Most of the things that we see around us are circular. Sun, moon on full moon day bangle mery-go around, which you loved so much when you where a child; all happened to circles. Ever wondered how a circle can be represented mathematically; well no!!, then we will tell you in this chapter. Also we will take about tangent normulas, chords which we all have hear about. So let us prove deep in to circles.
Definition: locus of a set of points equidistant from a fixed point Equation ofcircle -
(x - h)2+ (y - k)2 = r 2
x2h 2 - 2hx + y2 - 2ky + k2- r2 = 0
x2+ y2 + 2gx + 2fy + C = 0
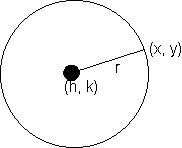
Center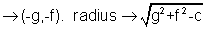
Genreal second degree equation-
ax2+ by2 + 2hxy + 2yx +2fy +C = 0
this equation refresent circle when,
a = b,h = 0 , g2 + f2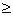
C
Equation of circle in different forms -
(1) Centre(h1K) radius a :-
(x - h)2 + (y - k)2 = a2
standard form (when center is origin):-
x2 + y2 = a2
(2).center (h,k)and pass through origin-
x2 + y2 - 2hx - 2ky = 0
Why :-
here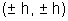
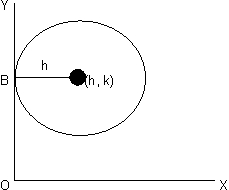
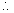(x - h)2 + (y - k)2 = r2 = h2 + k2
x2+ y2 - 2hx - 22ky = 0
Center(h,k) and touches the axis of x-y
x2+y2- 2hx - 2ky + h2= 0
(x - h)2 + (y - k)2 = k2
or, x2+ y2 - 2hx - l2ky + h2 = 0
(4)Center(h,k) and touches the axis of y-
x2 + y2-2hx -2ky + k2 = 0
Why :-
From fig it is clear that radius will be h .
(x - h)2 + (y - k)2 = h2
or, x2+ y2- 2hx - 2ky +k2 = 0
Circle which touches both the axis:-
Center will be(h, h)and radius will be h. But since center would be in any of the four quadrants its coordinates can be taken as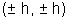
radius h.
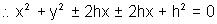
Illustration -1-. Find the equation of circle passing through (-2, 3) and touching both the axes.
Solution- As the circle toucher both theaxed and lies in 2ndquadrant, lits centre is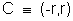
Where r is the radius , Distance of center from (- 2, 3) = radius .
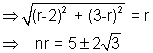
the circle are :- (x + r)2 + (y - r)2 = r2
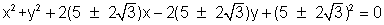
X2 + y2+ 2agx + 2fy +c = 0 ----equation of circle.
x intercept
Why :-
let it cut the axis x ie y = 0
in points (x2,0) and (x2, 0)
x1, x2 are the roots of x2 + 2yx + c = 0
x1, x2 = - 2y , x1 . x2 = c
Intercelt = x2 - x1
= [(x2 + x1)2- 4x 1x2] 1/2 =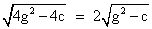
similarily .y intercept =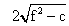
(6) Circle whose diameter is the line joining two point A (s1, y1 ) and B (x2, y2)-
Diametric form:-
(xx- x1)(x - x2) + (y - y1(y - y2) = 0
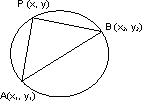
Why :-
Angle in a semicircle is a right angle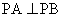
m1m2 = - 1
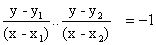
or (x - x1)(x - x2) + (y - y1)(y - y2) = 0
Definition: locus of a set of points equidistant from a fixed point Equation ofcircle -
(x - h)2+ (y - k)2 = r 2
x2h 2 - 2hx + y2 - 2ky + k2- r2 = 0
x2+ y2 + 2gx + 2fy + C = 0
Center
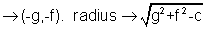
Genreal second degree equation-
ax2+ by2 + 2hxy + 2yx +2fy +C = 0
this equation refresent circle when,
a = b,h = 0 , g2 + f2
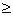CEquation of circle in different forms -
(1) Centre(h1K) radius a :-
(x - h)2 + (y - k)2 = a2
standard form (when center is origin):-
x2 + y2 = a2
(2).center (h,k)and pass through origin-
x2 + y2 - 2hx - 2ky = 0
Why :-
here
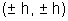
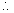(x - h)2 + (y - k)2 = r2 = h2 + k2x2+ y2 - 2hx - 22ky = 0
Center(h,k) and touches the axis of x-y
x2+y2- 2hx - 2ky + h2= 0
(x - h)2 + (y - k)2 = k2
or, x2+ y2 - 2hx - l2ky + h2 = 0
(4)Center(h,k) and touches the axis of y-
x2 + y2-2hx -2ky + k2 = 0
Why :-
From fig it is clear that radius will be h .
(x - h)2 + (y - k)2 = h2
or, x2+ y2- 2hx - 2ky +k2 = 0
Circle which touches both the axis:-
Center will be(h, h)and radius will be h. But since center would be in any of the four quadrants its coordinates can be taken as
radius h.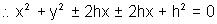Illustration -1-. Find the equation of circle passing through (-2, 3) and touching both the axes.
Solution- As the circle toucher both theaxed and lies in 2ndquadrant, lits centre is
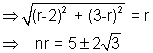
Where r is the radius , Distance of center from (- 2, 3) = radius .the circle are :- (x + r)2 + (y - r)2 = r2
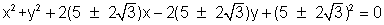
X2 + y2+ 2agx + 2fy +c = 0 ----equation of circle.
x intercept
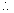
Why :-
let it cut the axis x ie y = 0
in points (x2,0) and (x2, 0)
x1, x2 are the roots of x2 + 2yx + c = 0x1, x2 = - 2y , x1 . x2 = cIntercelt = x2 - x1
= [(x2 + x1)2- 4x 1x2] 1/2 =
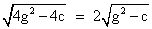
similarily .y intercept =
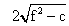
(6) Circle whose diameter is the line joining two point A (s1, y1 ) and B (x2, y2)-
Diametric form:-
(xx- x1)(x - x2) + (y - y1(y - y2) = 0
Why :-
Angle in a semicircle is a right angle
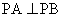
m1m2 = - 1
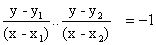
or (x - x1)(x - x2) + (y - y1)(y - y2) = 0