Circles - 2

(7) Parametric form-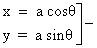
general point of a circle if centre is (0,0) isparameter (radius)


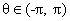
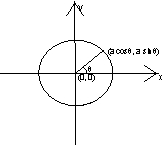
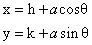
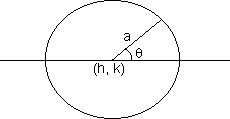
Illustration -2- Find the equation a circle which touches the .y axis at (0, 4) and cuts an intercept of length .6 units on x axis .
Solution- The equation of circle toching x = 0 at (0,4) can be taken as (x - 0)² + (y - 4² ) + kx = 0
x² + y² + kx - 8y + 16 = 0
the circle cuts x -axis point (x₁, 0) .8 (x₂, 0 )given by, x² + kx + 16 = 0
Xintercept difference of root of this quadratic equation 6 = | x₂ - x₁|
36 = (x₂ + x₁)² - 4x₁ .x₂

36 = k²- 4 (16)

k = 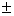10
Hence the required circle is ,
x² + y²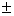10 x - 8y + 16 = 0

Some natations in a circle-

1. s = x² + y² + 2gx + 2fy + c
   
   
2. s₁= x x₁² + y₁² + 2yx₁ + 2fy₁ + c
   
   
3. T = xx₁ + yy₁ + g(x + x₁) + f (y + y₁) + c
   
   Standrad form-
   1)s = x² + y² - a ²
   
   2)s =₁x₁² + y₁ ² - a²
   
   
4. T = xx₁ + yy₁ - a2
   
   

• If s₁> 0 point lies out side the circle
  
• If s₁< 0 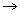point lies in side the circle
  
• If s₁ 0 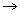point lies upon the circle
  
  Why :-
  Let equation of circle be X² + y² + 2yx + 2fy + c = 0
  having centre C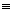( -y, -f) and radius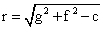
  Let P (x₁, y₁) be any point then :-
  P lies outside the circle if :-
  PC > r
  => x₁ ² + y₁² +2 yx ₁ + 2fy₁ + c > 0
  P lies on the circle if :-
  PC = r
  => x₁ ² + y₁² +2gx₁ +2fy ₁ + c = 0
  P lies inside the circle if :-
  PC < r
  => x₁² + y₁² +2gx₁ 2fy₁ + c < 0
  
  Dumb question :-
  How does PC > r leads to -
  x₁²+ y₁² + 2gx₁ + 2fy₁ + c > 0
  
  Ans-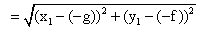
           
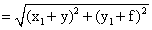
  and r =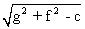
  Now PC > r
  => PC² > r²
  => (x₁ +y)²+(y₁ +f)² > y² + f ²- c
  => x₁² + y₁² 2gx, + 2fy₁ + c > 0
  (1) A line L and a circle intersed in two point A and B .
  => d < r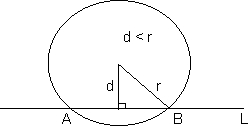
  => Perpendi cular distance of line L from the centre of circle is less than the radius, and the length of te chors AB is :-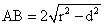
  
  (2) A line L and +a circle touch each other at a point P.
  => d = r
  => Perpendicular distance of L from the centre of circle = radius.
  (3) A line L and a circle may not intersect at all
  => .d > r
  => Perpendicular distance of line from the centre of circle is greater than the radius .
  (4) A line y = mx + c touches circle x² + y² = a²
  If :- perpendicular distance of line from centre of the circle
  = radius of the circle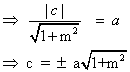
  
  Illustration- For what value of m, will line y = mx does not intersect the circle x²+y² + 20 X +20y + 20 = 0
  Solution- IF the line y = mx does not intersect the circle ; the perpendicular distance of the line from the centre of the circle must be greater than its radius .
  Centre of circle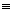 (-10, -10) ; radius
  distance of line mx - y = 0 from (-10, -10)
  => |m(-10)-(-10)|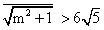
  
  =>(2m + 1) (m + 2) < 0
  => -2 < m < - 1/2
  Intersection of line with circle-
  Let the line be y = mx + d and circle is x²+ y² +2gx + 2fy + c
  thes x. Coordinate of their point of intersection are given by, (1 + m²)x2+ (2g + 2fm +2dm) x + d²+ 2fd + = o
  Why :-
  When the two curves intersect, both the curves will be simultaneously satisfied.
  So y = mx + d can be replaced in
  x²y² + 2gx + 2fy + c =0
  => x² + (mx + d )² + 2gx + 2f (mx + d) + c =0
  => (1 + m)² + (2g + 2fm + 2dm) x + d² + 2fd + c = 0
  if. (i) B² - 4AC = 0 then line touches the circle.
  (ii) B² - 4AC = > 0 then the line intersect circle at 2 different point.
  (iii) B² - 4AC = < 0 then no real intersecti takes place.
  
  Illustration 4- Find the point on the circle x² + y²
  = 4 whose distance from the line 4x + 3y = 12 is 4/5 .
  Soluction- Let A,B be the point on x²/u> + y² = 4 luing ar a distance 4/5 from 4x + 3y = 12
  => AB will be parallel to 4x + 3y = 12
  distance between the two line is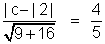
  => C = 16, 8
  => the equation of AB is :- 4x + 3y = 8 4x + 3y = 16
  the point A,B can be formed by sliving for point of intersection of x² y² = 4 with AB.
  AB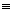(4x + 3y - 8 = 0)
  =>
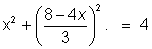
  => 25 x² - 64x + 28 = 0
  => x = 2, 14/25
  y = 0, 48/25
  AB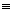 (4x + 3y - 16 = 0)
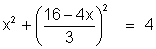  => => 25 x² - 128 x + 220 = 0
  => D < 0 => no real roots
  Hence these are two pointr on circle at distance 4/5 from liine
  A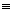(2,0) . & B 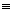(14/25, 48/25)