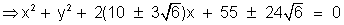Circles - 3

Alter native method -
let P 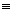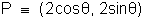be the point on the circle x² + y²= 4 distance . 4/5 from given line. the distsnce from line = 4/5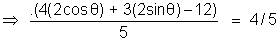

Solve for to get the point .
Equation of tangent in general form is :-
xx₁ + yy₁+ g(x + x₁) + f(y + y₁) + c = 0
equation of tangent on standard form :-
xx₁ + yy₁ a² = 0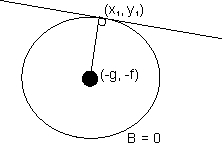


Why :-
Slope of tangent = -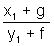
equation of tangent :-
y - y₁ - 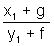(x - x₁)
(y - y₁) (y₁ + f) = - (x₁ + y) (x - x₁)
on solving we get,
xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + = 0
Equation of tangen 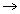T = 0 >
Dumb question- Why slope of tangent ?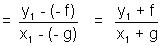
Ans - The slope of line Joining the centre to point of contact is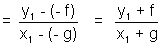

Now tangent os perpendicular to this line -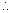
slope of tangent is -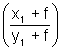
Note:- Golden rule to write equation of tangent is to replace. x² 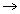xx₁, y² 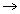yy 1
2x 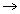x + x₁, 2y = y + y₁ in equation of circle where (x₁, y₁) is of contact.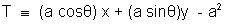



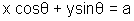
Equation of tangent.

Lngth of tangent:-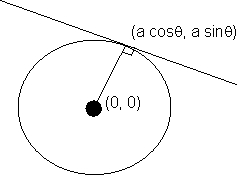



length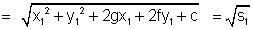
Why :-
let equation of circle be
x² + y² + 2gx + 2fy + c = 0
then center is c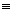(-g, -f) and radius = f
length of tangent = PA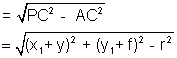


on solving we get ,
length of tangent
          
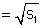
length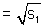
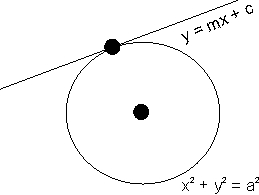
Condition of or line y = mx + c to be a ltangent to x²+ y² = a² -
Condition:-
c² = a² (1 + m²)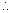
Equation of tangent:-
y = mx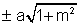


Why -?
putting y = mx + c in x² + y² = a²

x² + (mx + c)² = a²

(1 + m²) x² + 2mxc + c² - a² = 0

4m ² - c² -4 (c² - a² ) (1 + m²) = 0

c² = a²(1 + m²)

Similarily when circle equation is -
(x - h)² + (y - k)² = a²
equation of tangent with slope m
=> (y - k) = m (x - h)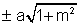

Dumb question :- Why D is taken zero ?

Ans- Line is touching circle.
It means on ksolving line and circle -
We will get only are solution -
It means quadratic of x will lhave repeated roots if means D = 0

Illustration- Find the equation of two tangents drawn to the circle x² + y² - 2x + 4y = 0 from point (0, 1)
Solution- let m be the slope of the tangent .
For true lengths here will be two values of m which are requited.
As the regent pases through (0, 1) its equation will be .
(y - 1) = m(x - 0)
mx - y + 1 = 0
Now the centre of circle (x² + y² - 2x + 4y = 0) is (1,-2) and radius r =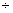
So using the condition of tangencu distance of centre (1, - 2) from line = radius (r)

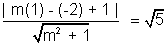=> m = 2, -1/2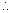

equation of tangents are :-
2x - y = 1 = 0 and x = 2y - 2 = 0
Illustration:- Find the equation mcircle passing through (-4, 3)an touching the line x + y = 2 and x - y = 2.
Solution .- let (h, k) be the centre of the circle the ditance of the centre from th given line and the given point must be equation to radius :-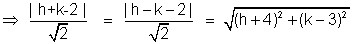


<>br /> Consider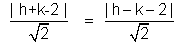
=> h + k - 2 = 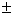(h - k - 2)
Case(I)- h + k - 2 = h - k -2 => k = 0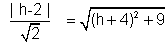

=> (h - 2)² = 2(h + 4)² + 18
=> h² + 20h + 46 = 0
=> k = 10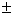
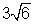
radius =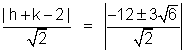
Circle is :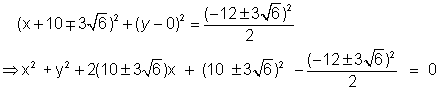



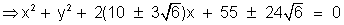
Case(II) - h + k - 2 = - (h - k - 2)
=> k² = 72 + 2 (k - 3)²
=> k² = 12 k + 90 = 0
The equation has no real roots. Hence no circle is possible for h = 2 .
Hence only two circle are possible (k = 0)