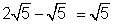Circles - 4
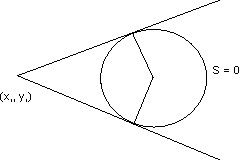
Pair of tangents -
T 2 = ss1
Equation of normal-
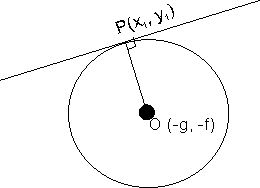
The normal to a curve at any P of a curve is the straight line which passes through P and is perpendicular to the tangent at P .
The equation of normal to the circle x2 + y2 + 2gx + 2fy + c = 0 at any point l(x1,y1) is :-
y(x1 + g) - x (y1 + f) +fx1 + gy1 = 0
Why :-
normal will be OP
slope OP =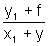
equation of normal -
on sloving we get,
y(x1 + y) - x(y1 + f) + fx1 - gy1 = 0
With respect to circle S = 0
Equation of chord of contact:-
T = 0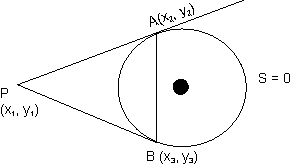
Why :-
Equation of circle S = 0
Whose, S = x2 + y2 - a2
Equation of AP => xx2 + yy2 - a2 = 0
Equation of BP => xx3 + yy3 - a2 = 0
Both passes through P .
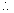x1x2+ y1y2 - a2 = 0 ..............(1)
x1x3+ y1y3 - a2 = 0 ..............(2)
Now consider
xx1+ yy1 - a2 = 0 ..............(3)
from (1), (2) and (3) it is lvery that clear that A and B
lies on (3)
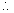equation of AB is 
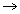xx1+ yy1 - a2 = 0
=> T = 0
Equation of chord lhaving mid point (x1, y1)
Only one such chord is possible
Equation of chord
T - s1 = 0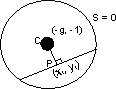
xx1+ yy1 +g(x + x1) + f (y + y1) + c
= x12 + y12 + 2gx1 + 2fy1 + c
Slop of CP = -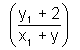
Equation of CP =>
(y - y1) = -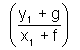
(x - x1)
on solving we get,
T = S1
T - S1 = 0
Illustration- Find the co-ordinates of the point from which tangen are drawn to the circle x2 + y2 - 6x - 4y + 3= 0 such that mid point of its chord of contact is (1, 1).
Ans- S = x2 + y2 - 6x - 4y + 3
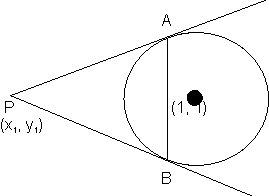
TAB = xx1 + yy1 - 3(x + x1) - 2(y1 + y1) + 3
(x1 - 3) x + (y1 - 2) y - 3x1 - 2y1 + 3= 0........(1)
Equation of AB T - S1 = 0
on solving
2x + y = 3 ............(2)
Comparing (1) and (2)
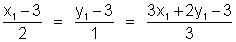
on solving, .
x1 = - 1, y1 = 0
In previous illastration why .
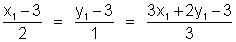
Why not x1 - 3 =2
y x1 - 3 =2 ?
Solution - On comparing two equation -
a1 x + b1y + c1 = 0
a2 x + b2y + c2 = 0
If both the above equation are of some line, then we get :-
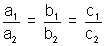
Two circle touching each other -
(a) External tiuch-
c1 c2 = r1 r2
Point P divides the line Joining c1 & c2 internally in th ratio
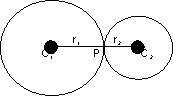
r1; r2
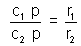
( b) Internal touch:-
c1 c2 = | r1 - r2|
point P divider the line Joining c1 & c2 externally in the ratio r1 : r2.
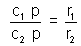
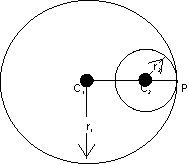
Conclition :-
|(r1 - r2)| < c1 c2 < r1 - r2
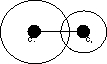
(a)One is completely inside other-
Conclition :-
c1c2 < r1 - r2
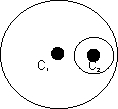
Illustration- Examine if the two circle x2 + y2 - 8y - 4 = 0 & x2 + y2 - 2x -4y = 0 touch each other find the point contact if they touch.
Solution- For x2 + y2 -2x - 4y = 0 centre c1
(1, 2)
& x2 + y2 -8x - 4 = 0 centre c2(0, 4)
using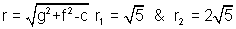
Now c1c2 =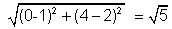
=> r2 - r1=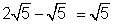
T 2 = ss1
Equation of normal-
The normal to a curve at any P of a curve is the straight line which passes through P and is perpendicular to the tangent at P .
The equation of normal to the circle x2 + y2 + 2gx + 2fy + c = 0 at any point l(x1,y1) is :-
y(x1 + g) - x (y1 + f) +fx1 + gy1 = 0
Why :-
normal will be OP
slope OP =
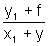
equation of normal -
on sloving we get,
y(x1 + y) - x(y1 + f) + fx1 - gy1 = 0
With respect to circle S = 0
Equation of chord of contact:-
T = 0
Why :-
Equation of circle S = 0
Whose, S = x2 + y2 - a2
Equation of AP => xx2 + yy2 - a2 = 0
Equation of BP => xx3 + yy3 - a2 = 0
Both passes through P .
x1x2+ y1y2 - a2 = 0 ..............(1)x1x3+ y1y3 - a2 = 0 ..............(2)
Now consider
xx1+ yy1 - a2 = 0 ..............(3)
from (1), (2) and (3) it is lvery that clear that A and B
lies on (3)
equation of AB is xx1+ yy1 - a2 = 0=> T = 0
Equation of chord lhaving mid point (x1, y1)
Only one such chord is possible
Equation of chord
T - s1 = 0
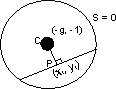
xx1+ yy1 +g(x + x1) + f (y + y1) + c
= x12 + y12 + 2gx1 + 2fy1 + c
Slop of CP = -
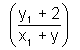
Equation of CP =>
(y - y1) = -
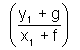(x - x1)on solving we get,
T = S1
T - S1 = 0
Illustration- Find the co-ordinates of the point from which tangen are drawn to the circle x2 + y2 - 6x - 4y + 3= 0 such that mid point of its chord of contact is (1, 1).
Ans- S = x2 + y2 - 6x - 4y + 3
TAB = xx1 + yy1 - 3(x + x1) - 2(y1 + y1) + 3
(x1 - 3) x + (y1 - 2) y - 3x1 - 2y1 + 3= 0........(1)
Equation of AB
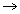T - S1 = 0on solving
2x + y = 3 ............(2)
Comparing (1) and (2)
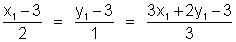
on solving, .
x1 = - 1, y1 = 0
In previous illastration why .
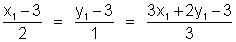
Why not x1 - 3 =2
y x1 - 3 =2 ?
Solution - On comparing two equation -
a1 x + b1y + c1 = 0
a2 x + b2y + c2 = 0
If both the above equation are of some line, then we get :-
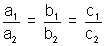
Two circle touching each other -
(a) External tiuch-
c1 c2 = r1 r2
Point P divides the line Joining c1 & c2 internally in th ratio
r1; r2
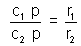
( b) Internal touch:-
c1 c2 = | r1 - r2|
point P divider the line Joining c1 & c2 externally in the ratio r1 : r2.
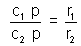
Conclition :-
|(r1 - r2)| < c1 c2 < r1 - r2
(a)One is completely inside other-
Conclition :-
c1c2 < r1 - r2
Illustration- Examine if the two circle x2 + y2 - 8y - 4 = 0 & x2 + y2 - 2x -4y = 0 touch each other find the point contact if they touch.
Solution- For x2 + y2 -2x - 4y = 0 centre c1
(1, 2)& x2 + y2 -8x - 4 = 0 centre c2
(0, 4)using
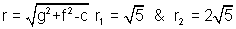
Now c1c2 =
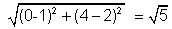
=> r2 - r1=