Circles - 5

For point of contact -
Let P(x, y) be the point of contact,
Pdivixles c₁c₂ externally in ratio of 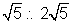= 1 : 2
using section formula, we get,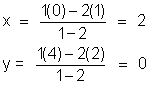

P(x, y)(2, 0) is the point of contact .

15 and touching the circle x² + y² = at point (6, 8).

solution- Case: It the required circle touches x² + y²
at (6, -8) centerally .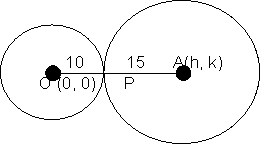


then P(6, -8) divider OA in the ratio 2 : 3 internally .
Let centre of the circle be (h, k). Now using section formula,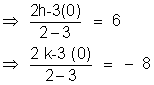


=> h = 15, & k = -20
=> (x - 15)² + (y + 20)² = 225 is the required circle .
Case-2 If the required circle touches x² + y² = 100 at (6, -8)internally, then P(6, - 8) divides oa in the ratio 2 : 3 exerternally .




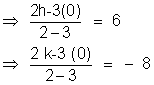
=> h = - 3 and k = 4
=> (x + 3d)² + (y - 4)² = 225 is the required circle .
(1) If two circle neither intersect nor touch eache other then they have 4 common tangents.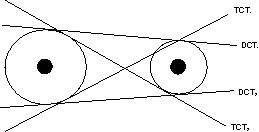



DCT means direct common tangent
TCT means Transverse common tangent .
(2) If two circle touch each other extenally then there are 3 common tangents .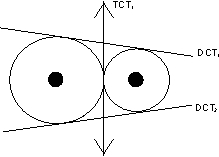



(3) If two circle intersect each other at 2 point then there are 2 common tangents.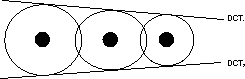



tangent is possible .



(5) If two circle are concentric then there is no common tangent between them .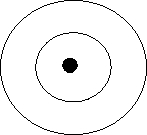



Director circle - The locus of meeting point of perpendicular two is also a circle concertric with the given circle is called director circle of the given circle .
Equation of given circle -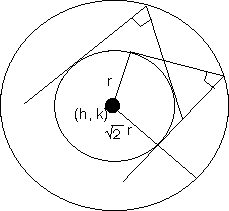



(x -h)² + (y -k)² = r²
Equation of director circle-
(x -h)² + (y -k)² = 2r²
Question- The line 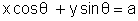and 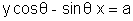meet at point (h, k) find the locus of point (h, k) for various values of .

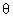Ans- Note that the line 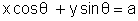and 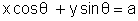are perpendicular to each othe and both are tangent to circle x² + y² = a² .
So, the locus of point of intersection of the two kof tangents ie, (h, k) is director circle with equation -
(1)Equatio of family of circle passing through point of intersection of a circle (s = 0) and a line (L =0) is given by -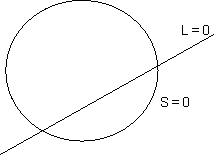



Illustration- Tangents PA and PB are drawn from the point P to circle x² + y² = a² . find the equation of circum circle ofPAB and the area of PAB.
sloution - AB is the chord of contact for point P.
Equation of AB is :-
hx + ky = a²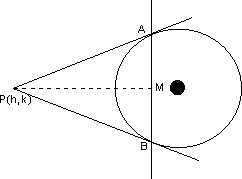



The circum circle of PAB passes through the intersection of circle. x² + y² - a² = 0 and the line hx + ky - a² = 0.
using S + KL = 0 (family of circle)
we can write equation of circle:-
(x² + y² - a² + k(hx + kg - a²) = 0 where k is paramete.
As this circle passes trough p(h, k);
=> h² + k² - a² + k(h² + k² - a²) = 0
=> k = - 1
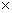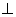The circle kis = 1/2 PM AB(PM AB)
PM = distance of p from AB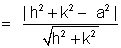

PA = length of tangent from P =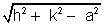
area =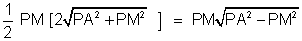
area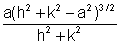

Note taht h² + k² - a² > 0
(h, k) lies outside the circle .
(2) Equation of family of circle passing through points of intersection of two given circle -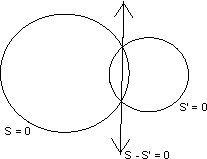



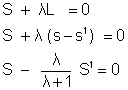
S + KS¹ = 0

(3) Equation of family of circle through .
two fixed given points .
S and L can be find out as fallows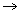


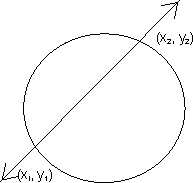
S = (x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0

(diametric form)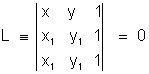


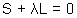
Illustration- Find the value of t so that the point (1, 1), (2, -1), (3, -2). and (12, t) are concyclic .

We will find the equatiion of the circle passing through A, B & C and then find t so that D lies on that circle .
Any circle passing through A, B can be taken as :-
(x - 1)(x - 2) + (y - 1)(y + 1) + K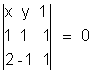
=> x² + y² - 3x + 1 + k (2x + y - 3) = 0
c(3, -2) lies on this circle .
=> 9 + 4 - 9 + 1 + k(6 - 2 - 3) = 0
=> k = - 5
=> circle through A; B & C is :-
x² + y² - 3x + 1 - 5 (2x + y - 3) = 0
x² + y² - 13x - 5y + 16 = 0
Point D (12, t) .will lie on this circle if :-
=> 144 + t² - 156 - 5t + 16 = 0
=> t² - 5t + 4 = 0
=> t = 1, 4
=> for t = 1, 4 the point are concyclic.

(4) Equation of family of circles through .
one point an a fixed given line-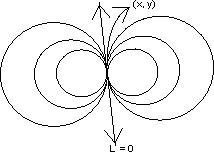


S = (x - x₁)² + (y - y₁)² = 0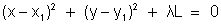

Illustration- Find the equation of a circle touching the line x + 2y = 1 at the point (3, - 1) and passing through the point (2, 1).
the point (3, 1) can be talen as :-
(x - 3)² + (y + 1)² + k(x + 2y - 1) = 0 (using family of circle )
As the circle passes through (2, 1)
(2 - 3)² + (1 + 1)² + k(2 + 2) = 0
=> k = - 5/3
=> the required circle is :-
3 (x² + y² - 23x - 4y + 35 = 0