Circles - 6

Orthognal cut of two circle-
If two circle are cutting each other orthogonally then the tangents at the point of intersection is perpendicular to each other :-


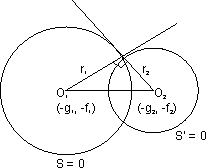
(O₁o₂)² = r₁² + r₂²

(g₁ - g₂)² + (f₁ - f₂)² = g₁² + f₁² - c₁ + g₂² + f₂² - c₁

2g₁g₂ + 2f₁f₂ = c₁ + c₂
Illustration - The center of circle S .line on the line 2x - 2y + 9 = 0 and S cuts at right anges the circle x² + y² = 4 . Show that S passes through two fixed point and fond heir coordinates
Contre lies on 2x - 2y + 9 = 0
=> - 2g + 2f + 9 = 0 ..........(1)
So cuts x² + y² - 4 = 0 orthogonally -
=> 2g (0) + 2f (0) = c - 4
=> c = 4 ...............(2)
Using (1) and (2) the equation of S be come :-
x² + y² + (2f + 9) x ++2fy + 4 = 0
=> (x² + y² + 9x + 4) + f(2x + 2y) = 0
We can compare this equation with the equation the family of circle through the point of interectin of a circle and a line (S + FL = 0, where f is a parameter).
Hence the circle S always pass through two fixed point A and B . Which are the point of intersection of x² + y² + 9x + 4 = 0 and 2x + 2y = 0
Solving these equation we get,
x² +xy² + 9x + 4 = 0
=> x = - 4, -1/2 => y = 4, 1/2
=>A (- 4, 4) & B (- 1/2, 1/2)

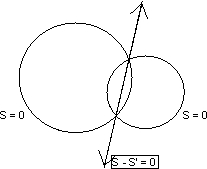
Radical axes- Locus of a point which moves such mthat mthe tangents drawn from tjhis point oto the two given circle will be of equal in lingth .

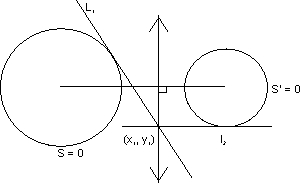
l₁ = l₂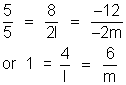


S₁ = S₁¹
equation of radical axes S₁ = S₁¹ = 0

Illustration- Find the equation of radical axes of the circle
S = x² + y² + 4x - 6y + 3 = 0
S¹ = 3x² + 3y² - 12x + 9y + 1 = 0

Ans- S₁ = S₁¹

=> x₁² + y₁² + 4x₁ - 6y₁ + 3 = x₁² + y₁² - 4x₁ + 3y₁ + 1/3

=> 24 x₁ - 27y₁ + 8 = 0
Important Results:-
(1)When circle are touching each other, the radical axes is the common tangent beween them.



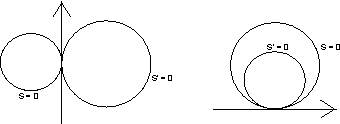
axes is common chord between them :-


Radical centre- If there are thre circle (whose centre are not clooinear.) then there will be three radical axes. All these three radical axes are concurrent . And the point of concurrency is called radical centre.
* Radical axes are perpendical to kthe line Joining centre of the circles .


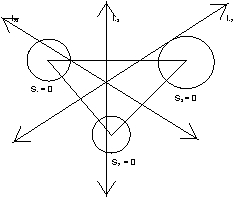
L₂₃S₂ -S₃ = 0

L₁₂ S₁ - S₂ = 0

adding above three -
L₁₃ = - (L₂₃ + L₁₂)
pair of lines.
Co axal System of circle-
A system of circle is said to be co axial when they have common radical axis ie, when radicaal axis of each pair of circles of system is same .

Illustration-
For what values of l and m the circle 5(x² + y²) + ly - m =0 belongs to the coaxal system determined by pthe circle .
x² + y² + 2x + 4y - 6 = 0 and 2² + y²) - x = 0 ?
Ans- If the radical axis for each pair of the three given circle is the same them the result is established.
Let the circle be .
S₁ = x² + y² + 2x + 4y - 6 = 0
S₂ = x² + y ² - 1/2 x = 0
S₃ = x² + y₂ + l/2y - m/5 = 0
the equation of radical axis of circle S₁ = 0, S₂ = 0 is S₁ - S₂ = 0
ie, x² + y² + 2x + 4y - 6 (x² + y² - 1/2x) = 0
or, 5/2x + 4y - 6 = 0
or, 5x + 8y - 12 = 0 ......................................................(1)
the equation of the radical axis of circle S₂ = 0, S₃ = 0 is S₂ - S₃ = 0
ie, x² + y² - 1/2x - (x² + y² + l/5y - m/5) = 0
or, 5x + 2ly - 2m = 0 .................................................(2)
(1) and (2) must be identical, so comparing them,

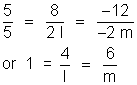
l = 4, m = 6
(Q | ) Find the equation of a circle which touches the line x + y = 5 at the point A(-2, 7) and cuts the circle x² + y² + 4x - 6y + 9 = 0 orthogonally .
(A |)
Since the circle is touching the line x + y - 5 = 0 at


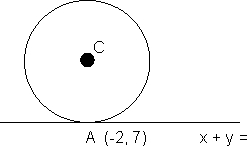
(-2, 7), its equation can be written as
(x + 2)² + (y - 7)² + K(x + y - 5) = 0 (whose k b vatiable
=> x² + y² + x (K + 4) + y(K -14) + 53 - 5 K = 0
It is orthogonal to the circle
x² + y² + 4x - 6y + 9 = 0
=> 2g₁ g₂ + 2f₁ f₂ = c₁ + c₂
=> 2(K + 4) - 3(K - 14) = 53 - 5 K + 9
4K = 12
K = 3
eqn of circle,
x² + y² + 7x - 11y + 38 = 0