Circles - 7

DUMB QUESTION
(Q) Why in this question we used family of circles and not did it directly by taking an an arbitrary circle and applying the given information ?
(A) Whenever it is given that kthe the circle is fouduing a line L and the point of contact P is also given, then always as e the following pointly.
(x - x₁)² + (y -y₁)² + K L = 0 K is variable .
It makes the solution very easy as only one variable is left and we have used 2 conditions namely
(a) Line L is tangent to circle.
(b) Point of coutact lis P .
So only are mose in formation is needed to define the circle .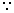
To define a circle we any three paramets
(Q2) Find the equation of circle passing through (- 2₁ 3) and touching both the axes.
(A2)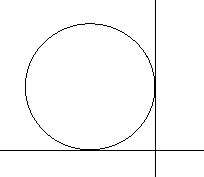


As the circle touches both the axes and lies in second quadeant, its contre is ;
C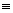(- r₁ r) where r is the radius.
Distance of contre from (- 2, 3) = eadius.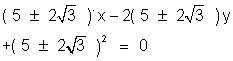

The circles we (x + r)² + (y - r)² = r²
(Q3) If 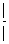; i =1,2,3,4 are four distinct points on a circle, show that m₁ m₂ m₃ m₄ = 1
Let the eqn of circle be
x² + y² + 2gx + 2fy + c = 0
Now since 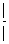is on the circle,

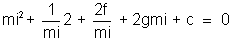
=> mi⁴ + 2g mi³ + cmi² + 2f mi + 1 = 0
The roots of this on are (m₁,m₂, m₃, m₄)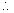
Product of the roots m₁,m₂, m₃, m₄ = = 1
Hence prooved .
Dumb question
(Q) Why are the roots of the above equation m₁,m₂, m₃,
m₄and how is m₁,m₂, m₃, m₄=18

(A) Since
individually satiefy the equation of circle, hence they all must be the solution of m : . And hence it is equation of degree 4. For a fore degree eqn ax⁴ + bx³ + cx² + dx + e = 0 .
product of roots = e/a .
m₁,m₂, m₃, m₄ = 1.
(Q4) For what value of m, will the line y = mx does not intersect the circle
x² + y² + 20x + 20y + 20 = 0
(A4) If the line y = m, does not ointersect the circle, the perpendicular distance of the line from the contre must be greater than its radius.
Contre of the circle (- 10, - 10); radius 6r = 61.
distance of the line mx - y = 0 from (- 10, - 10) .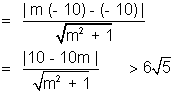

= (2m + 1)(m + 2) < 0
=> - 2 < m < - 1/2
(Q5) Secants are drawn from origin to the circle (x - h)² + (y - k)² = r². Find the locus of the mid - point of the portion of secants intercept inside the circle.
(A5)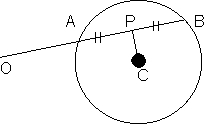

Let C(h₁ k) be the centre of the given circle . and P(x₁, y₁) be the mid point of the postion AB of the secant O AB.
=>
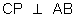
Slope COP) 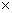slope(CP) = - 1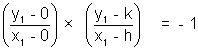

=> x₁² + y₁² - hx₁ - ky₁ = 0
the locus of the poine P : x² + y² - hx - ky = 0
A circle has radius equal to 3 units and its centre lies the line y = x - 1 . Find the equation of the circle if it passes through (7, 3) .
Ans - Let the centre of the circle be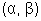
It lies of the line y = x - 1
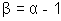=> . Hence the centre is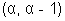
=> The equation of the circle is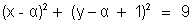

It passes through (7, 3)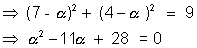


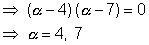
Hence the required equation are,
x² + y² - 8x - 6y + 16 = 0
and x² + y² - 14x - 12y + 76 = 0

Que - Prove that the circle x² + y² - 6x - 4y + 9 = 0 bisects the circumference of lthe circle.x² + y²- 8x - 6y + 23 = 0

Ans The given circles are
S₁x² + y² - 6x - 4y + 9 = 0 ………………………………….(1)
and S₂x² + y² - 8x - 6x + 23 = 0 ……………………………(2)
Equation of the common chord of circle (1) and (2) which is also the radical axis of the circle S₁ and ₂ is,
S₁ - S₂ = 0 or 2x + 2y - 14 = 0
or x + y - 7 = 0 …….(3)
Centre if the circle S₂ is (4, 3). clearly, line (3) passes through h point (4, 3) and hence line (3) is equation of diameter of circle (2)
Hance circle (1) bisects the circumfrance of circle(2)
extesnally. Find the angle beween the direct common tangents it given that r₁ > r₂.
Ans - let us draw the diagram.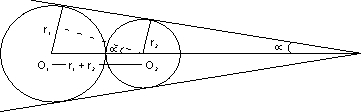



Cleatly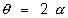

Now,




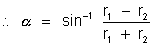
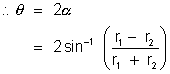
Q. Find th number of common tangents that can be drawn to circle x² + y² - 4x - 6y - 3 = 0
and x² + y² + 2x + 2y + 1 = 0 ?
Ans. The circle x² + y² - 4x - 6y - 3 = 0 has
Centre C₁ (2, 3) and radius r₁ = 4.
And the circle x² + y² + 2x + 2y + 1 = 0 has
Centre C₂ (-1, -1) and radius r₂ = 1

Now C₁C₂ =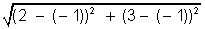
= 5
Also r₁ + r₂ = 4 + 1 = 5 .
So, the two circle touch each other externally and thus 3 common tangents are possible.

Q. If two circle cut the third circle orthogonally, prove that their common chord will pass through centre of third circle.
Ans. Let us take equation of two circle as .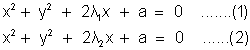


Let third circle be x² + y² + 2fy + c = 0 ……………………………….(3)
The circle (1) and (3) cut orthergonally .
So, 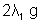= a + c. ……………………………..(4)
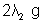= a + c. …………………………………(5)
from (4) and (5)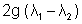
= 0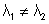
, as then circles would be same
So, g = 0
centre of third is (0, -f)
The common chord of (1) and (2) has equation S₁ - S₂
i.e x² + y² + 2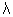₁x + a - (x² + y² + 2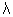₂x + a) = 0
=> 2(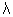₁ - 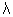₂)x = 0
or x = 0
So centre (0, - f) satisfies equation x = 0.